在Python开发过程中，你是否遇到过这样的困惑：为什么有时候函数返回None？什么时候应该使用None作为默认值？None到底是什么？作为Python开发者，理解None的本质和正确使用方式是提升代码质量的关键一步。

本文将深入解析Python中最特殊的数据类型——None，从单例模式的设计原理到实际开发中的最佳实践，帮你彻底掌握None的使用技巧，让你的Python代码更加专业和高效。

🔍 什么是None？揭开Python单例的神秘面纱

None的本质特征

None是Python中的一个特殊常量，代表"无"或"空值"的概念。它有以下几个重要特征：

Python
# None的类型
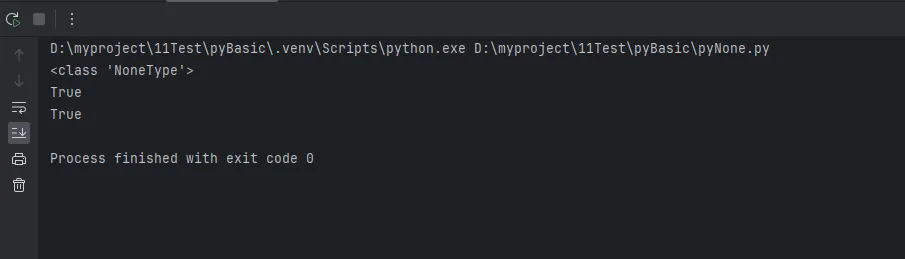
print(type(None))  # <class 'NoneType'>

# None是单例对象
a = None
b = None
print(a is b)  # True
print(id(a) == id(b))  # True，内存地址相同

关键特性：

• None是NoneType类的唯一实例
• 在整个Python程序中，所有的None都指向同一个对象
• None是不可变的（immutable）
• None在布尔上下文中被视为False

🎯 单例模式的优势

Python将None设计为单例模式有以下优势：

Python
import sys

# 验证None的单例特性
none_list = [None for _ in range(1000)]
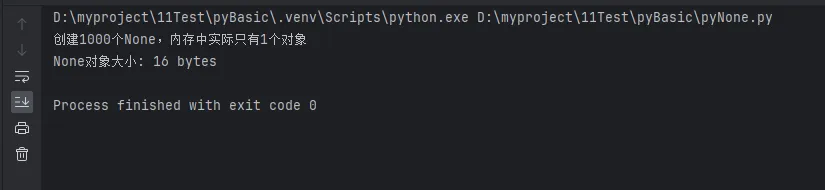
print(f"创建1000个None，内存中实际只有{len(set(id(n) for n in none_list))}个对象")

# 内存效率对比
print(f"None对象大小: {sys.getsizeof(None)} bytes")

在Python开发中，布尔类型(bool)看似简单，只有True和False两个值，但它却是程序逻辑控制的基石。无论是条件判断、循环控制，还是函数返回值的设计，布尔类型都发挥着举足轻重的作用。

很多初学者在使用布尔类型时，往往只停留在基础的True/False判断上，却忽略了Python中强大的布尔上下文机制和短路逻辑特性。这些高级特性不仅能让代码更加优雅简洁，还能显著提升程序性能。

本文将从实战角度深入解析Python布尔类型的三大核心应用：基础布尔操作、布尔上下文的灵活运用以及短路逻辑的性能优化，帮助你全面掌握这个看似简单却功能强大的数据类型。

🔍 问题分析：布尔类型的常见误区

在Windows应用开发中，我经常看到开发者对布尔类型的使用存在以下误区：

误区一：认为布尔类型只能存储True/False

误区二：不理解Python的布尔上下文机制

误区三：忽略短路逻辑带来的性能优势

让我们通过实际代码来分析这些问题。

💡 解决方案：布尔类型的三大核心特性

🎯 特性一：布尔类型的本质与创建

Python
# 布尔类型的创建方式
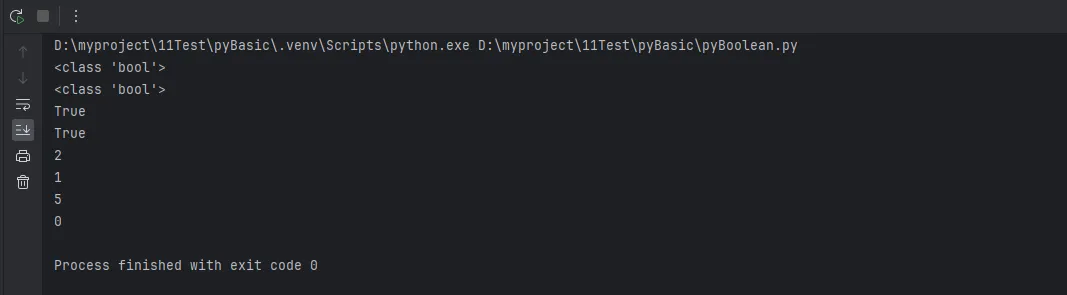
print(type(True))   # <class 'bool'>
print(type(False))  # <class 'bool'>

# 布尔类型继承自int
print(isinstance(True, int))   # True
print(isinstance(False, int))  # True

# 布尔值的数值表示
print(True + 1)    # 2
print(False + 1)   # 1
print(True * 5)    # 5
print(False * 5)   # 0

作为一名Python开发者，你是否曾经好奇过Python中那个看似"高大上"的复数类型？在日常的业务开发中，我们经常接触到整数、浮点数、字符串等基本数据类型，但复数却显得有些神秘。

实际上，复数在科学计算、信号处理、图像处理等领域有着广泛的应用。特别是在做上位机开发、数据分析或者科学计算时，掌握复数的使用技巧能让你的代码更加优雅高效。

本文将带你深入了解Python中复数的a + bj表示法、基本运算以及实际应用场景，让这个看似复杂的数据类型变得简单易懂！

🔍 问题分析：为什么需要复数？

数学背景回顾

在数学中，复数是由实部和虚部组成的数，通常表示为 a + bi 的形式，其中：

• a 是实部（Real Part）
• b 是虚部（Imaginary Part）
• i 是虚数单位，满足 i² = -1

在Python中，虚数单位用 j 表示（这是电子工程中的惯例），所以复数表示为 a + bj。

实际应用场景

• 信号处理：频域分析、傅里叶变换
• 电子工程：交流电路分析、阻抗计算
• 图像处理：频域滤波、图像变换
• 科学计算：量子力学计算、数值分析

💡 解决方案：Python复数完全指南

🚀 复数的创建方法

Python提供了多种创建复数的方式：

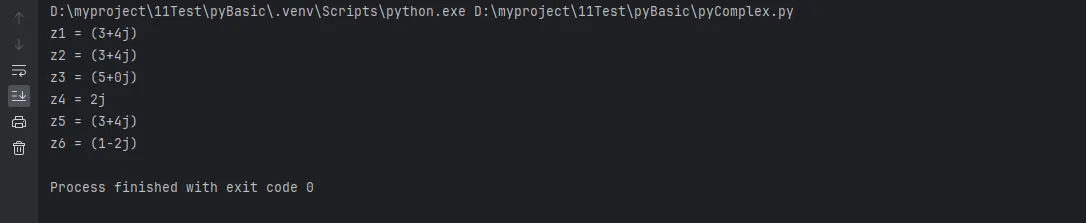
Python
# 方法1: 直接使用 a + bj 表示法
z1 = 3 + 4j
print(f"z1 = {z1}") 

# 方法2: 使用 complex() 函数
z2 = complex(3, 4)    # 实部3，虚部4
z3 = complex(5)       # 实部5，虚部0
z4 = complex(0, 2)    # 实部0，虚部2

print(f"z2 = {z2}") 
print(f"z3 = {z3}")
print(f"z4 = {z4}") 

# 方法3: 从字符串创建
z5 = complex("3+4j")
z6 = complex("1-2j")
print(f"z5 = {z5}") 
print(f"z6 = {z6}") 

你是否遇到过这样的奇怪现象：0.1 + 0.2 在Python中竟然不等于 0.3？或者在Windows应用开发中，浮点数计算结果总是出现微小的偏差，导致程序逻辑出错？这些看似简单的浮点数问题，实际上涉及到计算机底层的IEEE 754标准和浮点数精度处理机制。

作为Python开发者，特别是在上位机开发和数据处理场景中，深入理解浮点数的工作原理和精度问题至关重要。本文将从IEEE 754标准入手，全面解析Python浮点数的精度问题，并提供实用的解决方案，让你彻底掌握浮点数的正确使用方法。

🔬 问题分析：为什么浮点数计算会出现精度问题？

💻 IEEE 754标准详解

Python中的float类型遵循IEEE 754标准，这是一个国际标准，定义了浮点数在计算机中的存储和运算规则。

Python
import sys
import struct

# 查看Python浮点数的基本信息
print(f"Python浮点数信息：{sys.float_info}")
print(f"机器精度（机器ε）：{sys.float_info.epsilon}")
print(f"最大有限浮点数：{sys.float_info.max}")
print(f"最小正常化浮点数：{sys.float_info.min}")

IEEE 754双精度浮点数（Python默认）采用64位存储：

• 符号位：1位，表示正负
• 指数位：11位，表示数值范围
• 尾数位：52位，决定精度

🎭 精度问题的根本原因

Python
# 经典的浮点数精度问题演示
def demonstrate_float_precision():
    """演示浮点数精度问题"""
    
    # 案例1：简单的加法运算
    result1 = 0.1 + 0.2
    print(f"0.1 + 0.2 = {result1}")
    print(f"结果是否等于0.3？{result1 == 0.3}")
    print(f"实际值：{result1:.17f}")
    print(f"期望值：{0.3:.17f}")
    print("-" * 50)
    
    # 案例2：累积误差
    total = 0.0
    for i in range(10):
        total += 0.1
    print(f"0.1累加10次的结果：{total:.17f}")
    print(f"是否等于1.0？{total == 1.0}")
    print("-" * 50)
    
    # 案例3：二进制表示问题
    numbers = [0.1, 0.2, 0.3]
    for num in numbers:
        binary = format(struct.unpack('!Q', struct.pack('!d', num))[0], '064b')
        print(f"{num} 的二进制表示：{binary}")

demonstrate_float_precision()

输出结果分析：

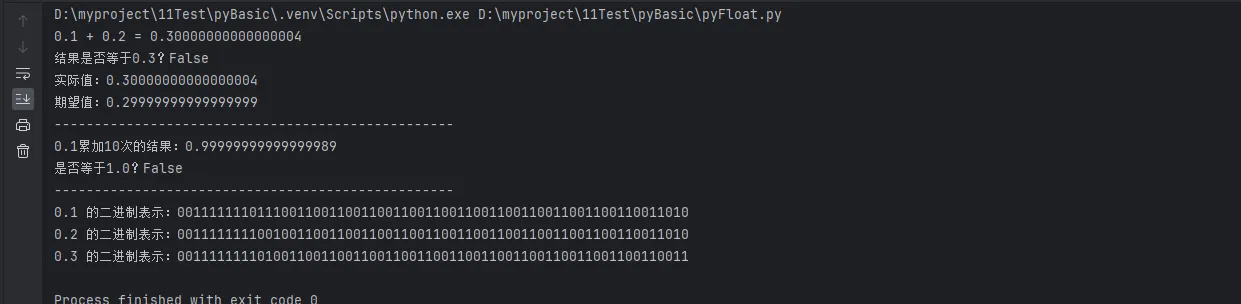
🔍 深入理解：十进制与二进制转换

在Python开发的世界里，整数(int)看似简单，但却蕴含着强大的功能。无论你是刚入门的新手，还是经验丰富的开发者，都可能在整数处理上遇到困惑：为什么Python的整数可以无限大？二进制、八进制、十六进制到底怎么用？在Windows下做上位机开发时，如何高效处理各种进制的数据？

本文将带你深入了解Python整数的核心特性，掌握任意精度计算、进制转换等实战技巧，让你在面对复杂的数值计算和数据处理时游刃有余。

🔍 Python整数的独特之处

任意精度：告别整数溢出的烦恼

与C++、Java等语言不同，Python的整数类型支持任意精度，这意味着你永远不用担心整数溢出问题。

Python
# 在其他语言中可能溢出的超大数
big_number = 123456789012345678901234567890
print(f"超大数: {big_number}")
print(f"类型: {type(big_number)}")

# 进行大数运算
result = big_number ** 10
print(f"10次方结果的位数: {len(str(result))}")

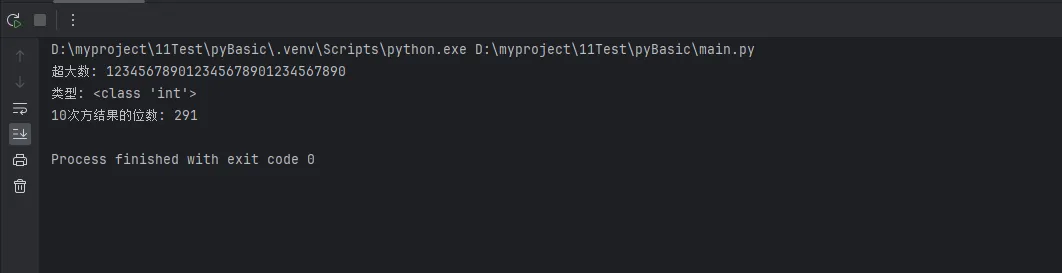
实战应用场景：

• 金融计算：处理大额资金时避免精度丢失
• 密码学：RSA加密中的大素数运算
• 上位机开发：处理传感器的超高精度数据

🎯 内存优化：小整数池机制

Python为了提高性能，对小整数（-5到256）使用了对象池技术：

Python
# 小整数对象复用演示
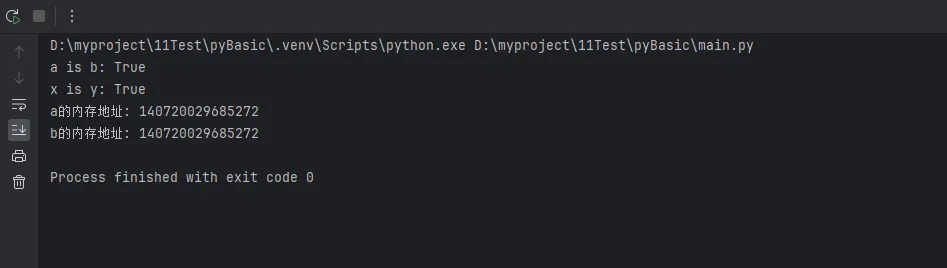
a = 100
b = 100
print(f"a is b: {a is b}")  # True，指向同一对象

# 大整数每次创建新对象
x = 1000
y = 1000
print(f"x is y: {x is y}")  # False，不同对象

# 验证对象ID
print(f"a的内存地址: {id(a)}")
print(f"b的内存地址: {id(b)}")