目录
作为一名Python开发者,你是否曾经好奇过Python中那个看似"高大上"的复数类型?在日常的业务开发中,我们经常接触到整数、浮点数、字符串等基本数据类型,但复数却显得有些神秘。
实际上,复数在科学计算、信号处理、图像处理等领域有着广泛的应用。特别是在做上位机开发、数据分析或者科学计算时,掌握复数的使用技巧能让你的代码更加优雅高效。
本文将带你深入了解Python中复数的a + bj表示法、基本运算以及实际应用场景,让这个看似复杂的数据类型变得简单易懂!
🔍 问题分析:为什么需要复数?
数学背景回顾
在数学中,复数是由实部和虚部组成的数,通常表示为 a + bi 的形式,其中:
a是实部(Real Part)b是虚部(Imaginary Part)i是虚数单位,满足 i² = -1
在Python中,虚数单位用 j 表示(这是电子工程中的惯例),所以复数表示为 a + bj。
实际应用场景
- 信号处理:频域分析、傅里叶变换
- 电子工程:交流电路分析、阻抗计算
- 图像处理:频域滤波、图像变换
- 科学计算:量子力学计算、数值分析
💡 解决方案:Python复数完全指南
🚀 复数的创建方法
Python提供了多种创建复数的方式:
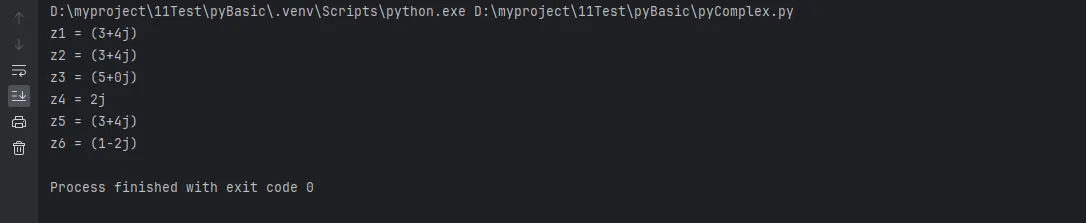
Python# 方法1: 直接使用 a + bj 表示法
z1 = 3 + 4j
print(f"z1 = {z1}")
# 方法2: 使用 complex() 函数
z2 = complex(3, 4) # 实部3,虚部4
z3 = complex(5) # 实部5,虚部0
z4 = complex(0, 2) # 实部0,虚部2
print(f"z2 = {z2}")
print(f"z3 = {z3}")
print(f"z4 = {z4}")
# 方法3: 从字符串创建
z5 = complex("3+4j")
z6 = complex("1-2j")
print(f"z5 = {z5}")
print(f"z6 = {z6}")
🎯 复数的属性访问
Pythonz = 3 + 4j
# 获取实部和虚部
print(f"实部: {z.real}")
print(f"虚部: {z.imag}")
# 注意:real和imag属性是只读的
# z.real = 5 # 这会报错!
# 获取复数的共轭
print(f"共轭: {z.conjugate()}")

⚡ 复数的基本运算
四则运算
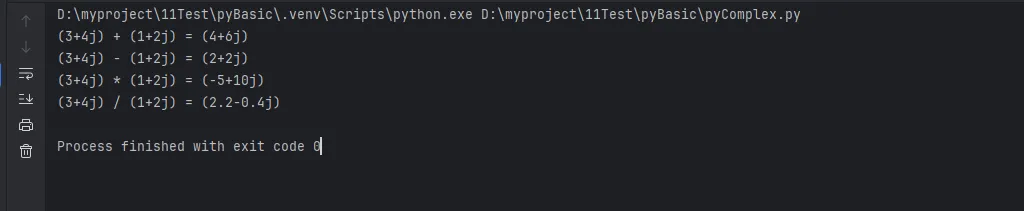
Pythonz1 = 3 + 4j
z2 = 1 + 2j
# 加法
add_result = z1 + z2
print(f"{z1} + {z2} = {add_result}")
# 减法
sub_result = z1 - z2
print(f"{z1} - {z2} = {sub_result}")
# 乘法
mul_result = z1 * z2
print(f"{z1} * {z2} = {mul_result}")
# 除法
div_result = z1 / z2
print(f"{z1} / {z2} = {div_result}")
幂运算
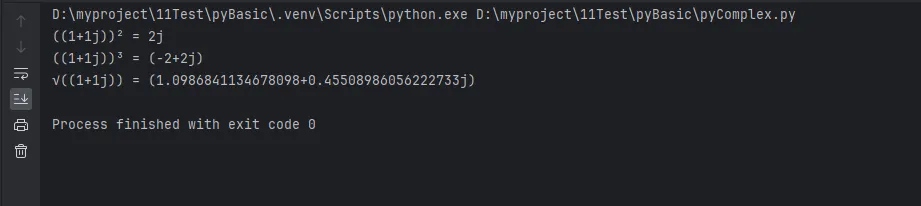
Pythonz = 1 + 1j
# 平方
square = z ** 2
print(f"({z})² = {square}")
# 立方
cube = z ** 3
print(f"({z})³ = {cube}")
# 开方
sqrt_result = z ** 0.5
print(f"√({z}) = {sqrt_result}")
📊 复数的模长和幅角
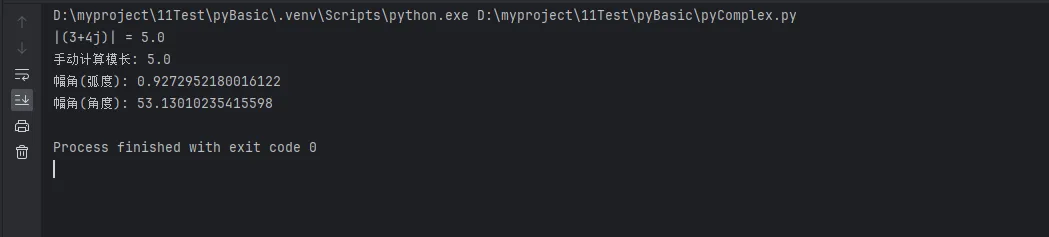
Pythonimport math
z = 3 + 4j
# 计算模长(绝对值)
modulus = abs(z)
print(f"|{z}| = {modulus}")
# 手动计算模长验证
manual_modulus = math.sqrt(z.real**2 + z.imag**2)
print(f"手动计算模长: {manual_modulus}")
# 计算幅角(需要导入cmath模块)
import cmath
phase = cmath.phase(z)
print(f"幅角(弧度): {phase}")
print(f"幅角(角度): {math.degrees(phase)}")
🛠️ 代码实战:实际应用案例
🔥 案例1:电路阻抗计算
在电子工程中,交流电路的阻抗可以用复数表示:
Pythonimport cmath
import math
def calculate_impedance(R, L, C, frequency):
"""
计算RLC电路的阻抗
R: 电阻(Ω)
L: 电感(H)
C: 电容(F)
frequency: 频率(Hz)
"""
omega = 2 * math.pi * frequency # 角频率
# 电阻阻抗
Z_R = complex(R, 0)
# 电感阻抗
Z_L = complex(0, omega * L)
# 电容阻抗
Z_C = complex(0, -1 / (omega * C))
# 总阻抗(串联)
Z_total = Z_R + Z_L + Z_C
return Z_total
# 实例计算
R = 100 # 100Ω电阻
L = 0.01 # 10mH电感
C = 1e-6 # 1μF电容
f = 1000 # 1kHz频率
impedance = calculate_impedance(R, L, C, f)
print(f"总阻抗: {impedance}")
print(f"阻抗模长: {abs(impedance):.2f}Ω")
print(f"相位角: {math.degrees(cmath.phase(impedance)):.2f}°")

🌊 案例2:信号生成与分析
Pythonimport numpy as np
import matplotlib.pyplot as plt
def generate_complex_signal(amplitude, frequency, phase, duration, sample_rate):
"""
生成复数信号
"""
t = np.linspace(0, duration, int(sample_rate * duration))
# 复指数信号: A * e^(j*(2πft + φ))
signal = amplitude * np.exp(1j * (2 * np.pi * frequency * t + phase))
return t, signal
# 生成信号
t, signal = generate_complex_signal(
amplitude=2,
frequency=5,
phase=np.pi/4,
duration=2,
sample_rate=100
)
# 分析信号
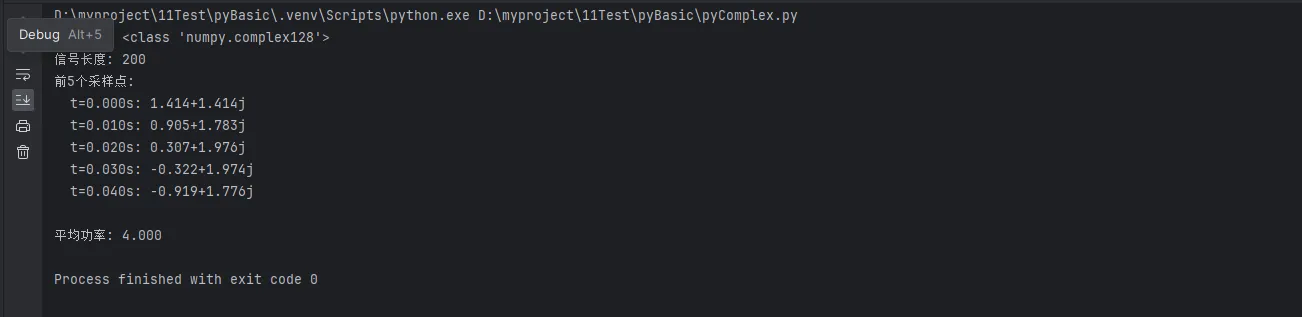
print(f"信号类型: {type(signal[0])}")
print(f"信号长度: {len(signal)}")
print(f"前5个采样点:")
for i in range(5):
print(f" t={t[i]:.3f}s: {signal[i]:.3f}")
# 计算功率
power = np.mean(np.abs(signal)**2)
print(f"\n平均功率: {power:.3f}")
🧮 案例3:复数运算工具类
Pythonimport math
class ComplexCalculator:
"""复数计算工具类"""
@staticmethod
def polar_to_rectangular(r, theta_degrees):
"""极坐标转直角坐标"""
theta_radians = math.radians(theta_degrees)
real = r * math.cos(theta_radians)
imag = r * math.sin(theta_radians)
return complex(real, imag)
@staticmethod
def rectangular_to_polar(z):
"""直角坐标转极坐标"""
r = abs(z)
theta_radians = cmath.phase(z)
theta_degrees = math.degrees(theta_radians)
return r, theta_degrees
@staticmethod
def nth_root(z, n):
"""计算复数的n次方根"""
r, theta = ComplexCalculator.rectangular_to_polar(z)
roots = []
for k in range(n):
root_r = r ** (1/n)
root_theta = (theta + 360 * k) / n
root = ComplexCalculator.polar_to_rectangular(root_r, root_theta)
roots.append(root)
return roots
# 使用示例
calc = ComplexCalculator()
# 极坐标转换
z1 = calc.polar_to_rectangular(5, 53.13)
print(f"极坐标(5, 53.13°) = {z1}")
# 直角坐标转换
r, theta = calc.rectangular_to_polar(3 + 4j)
print(f"直角坐标(3+4j) = 极坐标({r:.2f}, {theta:.2f}°)")
# 计算平方根
square_roots = calc.nth_root(16 + 0j, 2)
print(f"16的平方根: {square_roots}")
# 计算立方根
cube_roots = calc.nth_root(8 + 0j, 3)
print(f"8的立方根: {cube_roots}")

🎓 高级技巧与最佳实践
⚡ 性能优化技巧
Pythonimport time
import numpy as np
def performance_comparison():
"""比较不同复数操作的性能"""
# 创建测试数据
n = 1000000
real_parts = np.random.randn(n)
imag_parts = np.random.randn(n)
# 方法1:使用Python内置复数
start_time = time.time()
python_complex = [complex(r, i) for r, i in zip(real_parts, imag_parts)]
python_time = time.time() - start_time
# 方法2:使用NumPy复数数组
start_time = time.time()
numpy_complex = real_parts + 1j * imag_parts
numpy_time = time.time() - start_time
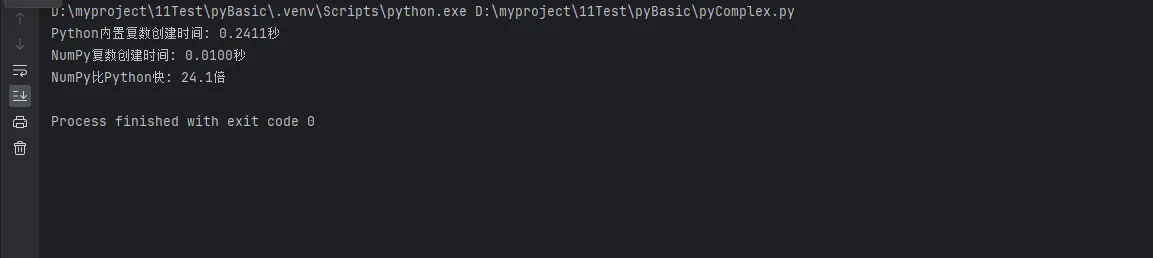
print(f"Python内置复数创建时间: {python_time:.4f}秒")
print(f"NumPy复数创建时间: {numpy_time:.4f}秒")
print(f"NumPy比Python快: {python_time/numpy_time:.1f}倍")
# 运行性能测试
performance_comparison()
🔧 调试与错误处理
Pythondef safe_complex_division(z1, z2):
"""安全的复数除法,包含错误处理"""
try:
if z2 == 0:
raise ZeroDivisionError("不能除以零复数")
result = z1 / z2
# 检查结果是否为有效复数
if math.isnan(result.real) or math.isnan(result.imag):
raise ValueError("计算结果包含NaN")
if math.isinf(result.real) or math.isinf(result.imag):
raise ValueError("计算结果为无穷大")
return result
except ZeroDivisionError as e:
print(f"除法错误: {e}")
return None
except ValueError as e:
print(f"数值错误: {e}")
return None
except Exception as e:
print(f"未知错误: {e}")
return None
# 测试错误处理
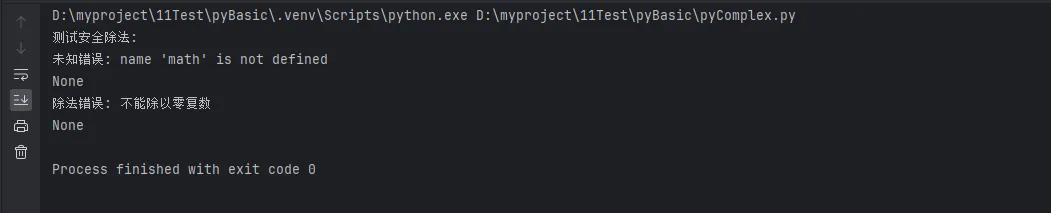
print("测试安全除法:")
print(safe_complex_division(1+2j, 2+3j))
print(safe_complex_division(1+2j, 0+0j))
📚 扩展学习建议
如果你想深入学习Python复数相关知识,建议关注以下方向:
- NumPy科学计算:学习如何高效处理复数数组
- SciPy信号处理:掌握FFT、滤波等高级应用
- Matplotlib数据可视化:学会绘制复数相关图形
- SymPy符号计算:进行复数的符号运算
🎯 总结核心要点
通过本文的深入解析,我们掌握了Python复数的三个核心要点:
- 基础语法掌握:熟练使用
a + bj表示法创建复数,理解real、imag属性和基本运算规则 - 实战应用能力:能够运用复数解决电路分析、信号处理、科学计算等实际问题,提升Python开发的专业性
- 性能优化意识:了解何时使用NumPy进行批量复数计算,掌握错误处理和调试技巧,写出更健壮的代码
掌握复数这个"看似高深"的数据类型,不仅能让你在科学计算领域游刃有余,更能在上位机开发、数据分析等工作中展现出扎实的Python编程技巧。记住,每一个看似复杂的概念,都有其简单实用的一面!
如果这篇文章对你有帮助,欢迎点赞收藏,让更多Python开发者一起进步!有问题欢迎在评论区讨论交流。
本文作者:技术老小子
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
目录