你是否遇到过这样的奇怪现象：0.1 + 0.2 在Python中竟然不等于 0.3？或者在Windows应用开发中，浮点数计算结果总是出现微小的偏差，导致程序逻辑出错？这些看似简单的浮点数问题，实际上涉及到计算机底层的IEEE 754标准和浮点数精度处理机制。

作为Python开发者，特别是在上位机开发和数据处理场景中，深入理解浮点数的工作原理和精度问题至关重要。本文将从IEEE 754标准入手，全面解析Python浮点数的精度问题，并提供实用的解决方案，让你彻底掌握浮点数的正确使用方法。

🔬 问题分析：为什么浮点数计算会出现精度问题？

💻 IEEE 754标准详解

Python中的float类型遵循IEEE 754标准，这是一个国际标准，定义了浮点数在计算机中的存储和运算规则。

Python
import sys
import struct

# 查看Python浮点数的基本信息
print(f"Python浮点数信息：{sys.float_info}")
print(f"机器精度（机器ε）：{sys.float_info.epsilon}")
print(f"最大有限浮点数：{sys.float_info.max}")
print(f"最小正常化浮点数：{sys.float_info.min}")

IEEE 754双精度浮点数（Python默认）采用64位存储：

• 符号位：1位，表示正负
• 指数位：11位，表示数值范围
• 尾数位：52位，决定精度

🎭 精度问题的根本原因

Python
# 经典的浮点数精度问题演示
def demonstrate_float_precision():
    """演示浮点数精度问题"""
    
    # 案例1：简单的加法运算
    result1 = 0.1 + 0.2
    print(f"0.1 + 0.2 = {result1}")
    print(f"结果是否等于0.3？{result1 == 0.3}")
    print(f"实际值：{result1:.17f}")
    print(f"期望值：{0.3:.17f}")
    print("-" * 50)
    
    # 案例2：累积误差
    total = 0.0
    for i in range(10):
        total += 0.1
    print(f"0.1累加10次的结果：{total:.17f}")
    print(f"是否等于1.0？{total == 1.0}")
    print("-" * 50)
    
    # 案例3：二进制表示问题
    numbers = [0.1, 0.2, 0.3]
    for num in numbers:
        binary = format(struct.unpack('!Q', struct.pack('!d', num))[0], '064b')
        print(f"{num} 的二进制表示：{binary}")

demonstrate_float_precision()

输出结果分析：

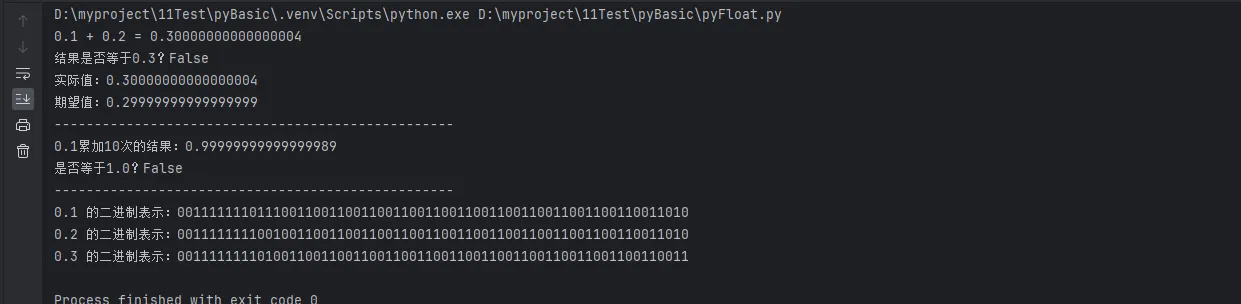
🔍 深入理解：十进制与二进制转换

Python
from fractions import Fraction
import decimal

def analyze_decimal_binary_conversion():
    """分析十进制与二进制转换问题"""
    
    # 0.1在计算机中的真实表示
    print("=== 0.1的真实表示 ===")
    
    # 使用Fraction显示精确的分数形式
    f = Fraction(0.1).limit_denominator()
    print(f"0.1作为分数：{f}")
    
    # 显示IEEE 754的实际存储值
    exact_fraction = Fraction(0.1)
    print(f"0.1的精确分数表示：{exact_fraction}")
    
    # 使用decimal模块获取精确值
    decimal.getcontext().prec = 50  # 设置高精度
    d = decimal.Decimal('0.1')
    print(f"高精度decimal表示：{d}")
    
    # 转换为二进制查看
    def float_to_binary_detailed(num):
        """详细显示浮点数的二进制分解"""
        packed = struct.pack('!d', num)
        bits = ''.join(f'{byte:08b}' for byte in packed)
        
        sign = bits[0]
        exponent = bits[1:12]
        mantissa = bits[12:]
        
        print(f"数值：{num}")
        print(f"符号位：{sign} ({'负' if sign == '1' else '正'})")
        print(f"指数位：{exponent} (十进制：{int(exponent, 2) - 1023})")
        print(f"尾数位：{mantissa[:20]}... (前20位)")
        
    float_to_binary_detailed(0.1)

analyze_decimal_binary_conversion()

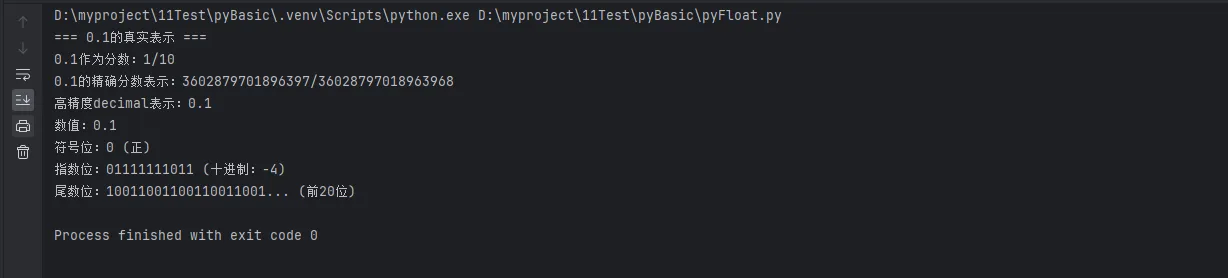
🛠️ 解决方案：正确处理浮点数精度

🎯 方案1：使用math.isclose()进行浮点数比较

Python
import sys
import struct

import math


class FloatComparison:
    """浮点数比较工具类"""

    def __init__(self, rel_tol=1e-09, abs_tol=0.0):
        """
        初始化比较参数
        rel_tol: 相对容差（默认1e-09）
        abs_tol: 绝对容差（默认0.0）
        """
        self.rel_tol = rel_tol
        self.abs_tol = abs_tol

    def is_equal(self, a, b, custom_rel_tol=None, custom_abs_tol=None):
        """安全的浮点数相等比较"""
        rel_tol = custom_rel_tol if custom_rel_tol is not None else self.rel_tol
        abs_tol = custom_abs_tol if custom_abs_tol is not None else self.abs_tol

        return math.isclose(a, b, rel_tol=rel_tol, abs_tol=abs_tol)

    def is_zero(self, value, tolerance=1e-10):
        """判断是否接近零"""
        return abs(value) < tolerance

    def round_to_significant_digits(self, value, digits):
        """保留指定有效数字"""
        if value == 0:
            return 0
        return round(value, digits - int(math.floor(math.log10(abs(value)))) - 1)


# 实际应用示例
def practical_float_comparison():
    """实际应用中的浮点数比较"""
    comparator = FloatComparison()

    # 测试用例1：基本运算比较
    result = 0.1 + 0.2
    expected = 0.3
    print(f"传统比较：{result} == {expected} -> {result == expected}")
    print(f"安全比较：math.isclose({result}, {expected}) -> {comparator.is_equal(result, expected)}")
    print()

    # 测试用例2：累积误差场景
    total = sum(0.1 for _ in range(10))
    print(f"累积结果：{total}")
    print(f"与1.0比较：{comparator.is_equal(total, 1.0)}")
    print()

    # 测试用例3：科学计算场景
    scientific_values = [
        (1e-10 + 1e-11, 1e-10, 1e-12),  # 很小的数值
        (1e10 + 1, 1e10, 1e-5),  # 很大的数值
    ]

    for a, b, tolerance in scientific_values:
        print(f"比较 {a} 和 {b}")
        print(f"默认参数：{math.isclose(a, b)}")
        print(f"自定义容差：{comparator.is_equal(a, b, custom_abs_tol=tolerance)}")
        print()


practical_float_comparison()

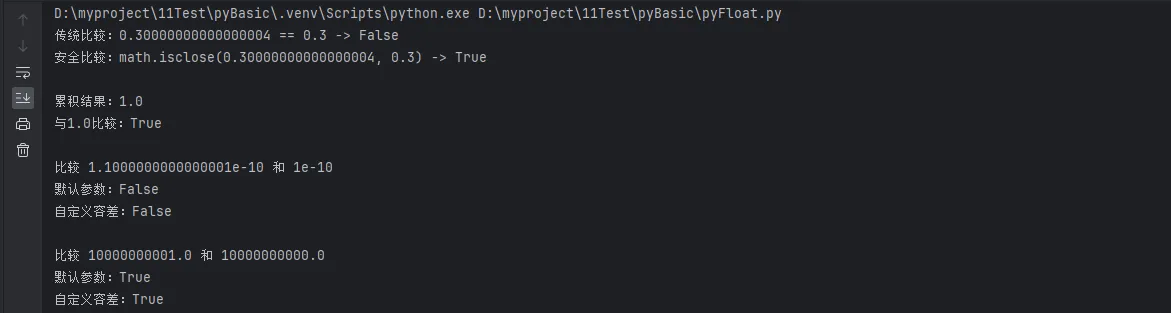
🔧 方案2：decimal模块实现高精度计算

Python
from decimal import Decimal, getcontext, ROUND_HALF_UP
import time

class PreciseCalculator:
    """高精度计算器"""
    
    def __init__(self, precision=28):
        """设置计算精度"""
        getcontext().prec = precision
        self.precision = precision
    
    def add(self, a, b):
        """精确加法"""
        return Decimal(str(a)) + Decimal(str(b))
    
    def subtract(self, a, b):
        """精确减法"""
        return Decimal(str(a)) - Decimal(str(b))
    
    def multiply(self, a, b):
        """精确乘法"""
        return Decimal(str(a)) * Decimal(str(b))
    
    def divide(self, a, b):
        """精确除法"""
        if b == 0:
            raise ValueError("除数不能为零")
        return Decimal(str(a)) / Decimal(str(b))
    
    def financial_round(self, value, decimal_places=2):
        """金融级四舍五入"""
        decimal_value = Decimal(str(value))
        return decimal_value.quantize(
            Decimal('0.' + '0' * decimal_places),
            rounding=ROUND_HALF_UP
        )
    
    def performance_test(self, iterations=100000):
        """性能测试：float vs decimal"""
        # float运算测试
        start_time = time.time()
        for i in range(iterations):
            result = 0.1 + 0.2 + 0.3
        float_time = time.time() - start_time
        
        # decimal运算测试
        start_time = time.time()
        d1, d2, d3 = Decimal('0.1'), Decimal('0.2'), Decimal('0.3')
        for i in range(iterations):
            result = d1 + d2 + d3
        decimal_time = time.time() - start_time
        
        print(f"=== 性能测试结果 ({iterations}次运算) ===")
        print(f"float运算时间：{float_time:.6f}秒")
        print(f"decimal运算时间：{decimal_time:.6f}秒")
        print(f"性能比率：decimal/float = {decimal_time/float_time:.2f}")

# 实战应用：金融计算系统
def financial_calculation_demo():
    """金融计算演示"""
    calc = PreciseCalculator(precision=10)
    
    print("=== 金融计算系统演示 ===")
    
    # 场景1：价格计算
    unit_price = "29.99"
    quantity = "3"
    tax_rate = "0.08"
    
    subtotal = calc.multiply(unit_price, quantity)
    tax = calc.multiply(subtotal, tax_rate)
    total = calc.add(subtotal, tax)
    
    print(f"单价：${unit_price}")
    print(f"数量：{quantity}")
    print(f"小计：${subtotal}")
    print(f"税费：${tax}")
    print(f"总计：${calc.financial_round(total)}")
    print()
    
    # 场景2：利息计算
    principal = "10000.00"
    annual_rate = "0.0425"
    years = "5"
    
    # 复利计算：A = P(1 + r)^t
    base = calc.add("1", annual_rate)
    power_result = Decimal(str(base)) ** int(years)
    final_amount = calc.multiply(principal, str(power_result))
    interest = calc.subtract(final_amount, principal)
    
    print(f"本金：${principal}")
    print(f"年利率：{float(annual_rate)*100}%")
    print(f"期限：{years}年")
    print(f"最终金额：${calc.financial_round(final_amount)}")
    print(f"利息收入：${calc.financial_round(interest)}")
    
    # 性能测试
    calc.performance_test()

financial_calculation_demo()

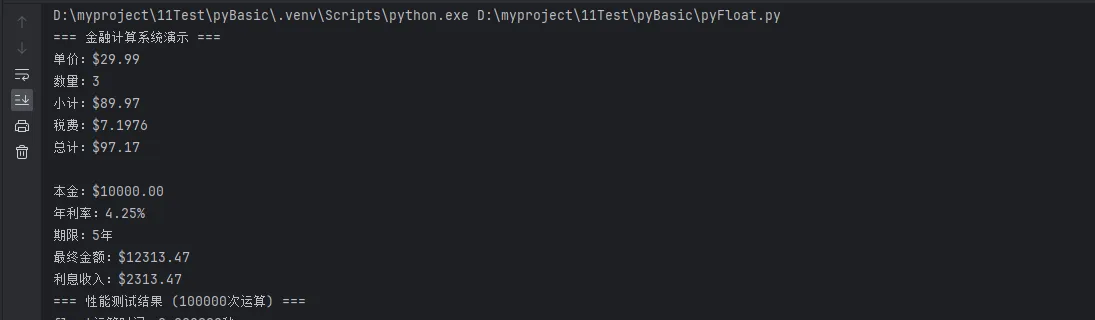
⚡ 方案3：自定义浮点数处理工具

Python
import math
from typing import Union, Optional

class SmartFloat:
    """智能浮点数处理类"""
    
    def __init__(self, value: Union[float, int, str], precision: int = 15):
        """
        初始化智能浮点数
        value: 数值
        precision: 显示精度
        """
        self.value = float(value)
        self.precision = precision
    
    def __str__(self):
        """字符串表示"""
        return f"{self.value:.{self.precision}g}"
    
    def __repr__(self):
        """调试表示"""
        return f"SmartFloat({self.value}, precision={self.precision})"
    
    def __add__(self, other):
        """加法运算"""
        if isinstance(other, SmartFloat):
            return SmartFloat(self.value + other.value, self.precision)
        return SmartFloat(self.value + float(other), self.precision)
    
    def __eq__(self, other):
        """相等比较"""
        if isinstance(other, SmartFloat):
            return math.isclose(self.value, other.value)
        return math.isclose(self.value, float(other))
    
    def __lt__(self, other):
        """小于比较"""
        other_val = other.value if isinstance(other, SmartFloat) else float(other)
        return self.value < other_val and not math.isclose(self.value, other_val)
    
    def close_to(self, other, rel_tol=1e-09, abs_tol=0.0):
        """自定义精度比较"""
        other_val = other.value if isinstance(other, SmartFloat) else float(other)
        return math.isclose(self.value, other_val, rel_tol=rel_tol, abs_tol=abs_tol)
    
    @classmethod
    def from_fraction(cls, numerator: int, denominator: int, precision: int = 15):
        """从分数创建"""
        return cls(numerator / denominator, precision)
    
    def to_rational_approximation(self, max_denominator: int = 1000000):
        """转换为有理数近似"""
        from fractions import Fraction
        return Fraction(self.value).limit_denominator(max_denominator)

# Windows上位机开发中的实际应用
def windows_application_demo():
    """Windows应用开发中的浮点数处理"""
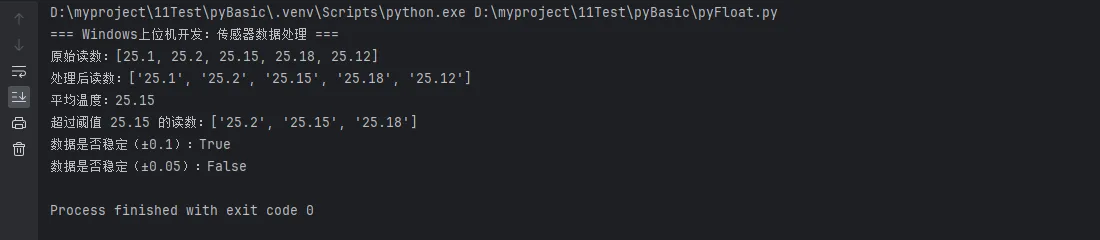
    print("=== Windows上位机开发：传感器数据处理 ===")
    
    # 模拟传感器读数（带有精度误差）
    temperature_readings = [25.1, 25.2, 25.15, 25.18, 25.12]
    
    # 使用SmartFloat处理
    smart_readings = [SmartFloat(reading) for reading in temperature_readings]
    
    # 计算平均值
    total = SmartFloat(0)
    for reading in smart_readings:
        total = total + reading
    
    average = SmartFloat(total.value / len(smart_readings))
    
    print(f"原始读数：{temperature_readings}")
    print(f"处理后读数：{[str(r) for r in smart_readings]}")
    print(f"平均温度：{average}")
    
    # 阈值检测
    threshold = SmartFloat(25.15)
    over_threshold = [r for r in smart_readings if not (r < threshold)]
    
    print(f"超过阈值 {threshold} 的读数：{[str(r) for r in over_threshold]}")
    
    # 数据稳定性检查
    def is_stable(readings, tolerance=0.1):
        """检查数据是否稳定"""
        if len(readings) < 2:
            return True
        
        for i in range(1, len(readings)):
            if not readings[i].close_to(readings[0], abs_tol=tolerance):
                return False
        return True
    
    print(f"数据是否稳定（±0.1）：{is_stable(smart_readings, 0.1)}")
    print(f"数据是否稳定（±0.05）：{is_stable(smart_readings, 0.05)}")

windows_application_demo()

💡 代码实战：构建完整的浮点数处理库

Python
import math
import sys
from typing import List, Tuple
from decimal import Decimal, getcontext

class FloatPrecisionManager:
    """浮点数精度管理器 - 完整解决方案"""
    
    def __init__(self):
        """初始化管理器"""
        self.default_rel_tol = 1e-09
        self.default_abs_tol = 0.0
        getcontext().prec = 28
    
    def safe_compare(self, a: float, b: float, 
                    rel_tol: float = None, abs_tol: float = None) -> bool:
        """安全的浮点数比较"""
        rel_tol = rel_tol or self.default_rel_tol
        abs_tol = abs_tol or self.default_abs_tol
        return math.isclose(a, b, rel_tol=rel_tol, abs_tol=abs_tol)
    
    def safe_sum(self, numbers: List[float]) -> float:
        """安全的浮点数求和（减少累积误差）"""
        # 使用Kahan求和算法
        total = 0.0
        compensation = 0.0
        
        for num in numbers:
            y = num - compensation
            temp = total + y
            compensation = (temp - total) - y
            total = temp
        
        return total
    
    def format_scientific(self, value: float, significant_digits: int = 6) -> str:
        """科学记数法格式化"""
        if value == 0:
            return "0.0"
        
        # 计算指数
        exponent = int(math.floor(math.log10(abs(value))))
        mantissa = value / (10 ** exponent)
        
        # 格式化尾数
        mantissa_str = f"{mantissa:.{significant_digits-1}f}"
        
        return f"{mantissa_str}e{exponent:+d}"
    
    def analyze_precision_loss(self, operation: str, 
                             operands: List[float]) -> dict:
        """分析精度损失"""
        result = {
            'operation': operation,
            'operands': operands,
            'float_result': None,
            'decimal_result': None,
            'precision_loss': None,
            'relative_error': None
        }
        
        try:
            # 使用float计算
            if operation == 'add':
                result['float_result'] = sum(operands)
            elif operation == 'multiply':
                float_result = 1.0
                for op in operands:
                    float_result *= op
                result['float_result'] = float_result
            
            # 使用Decimal计算（作为"真值"参考）
            decimal_operands = [Decimal(str(op)) for op in operands]
            if operation == 'add':
                result['decimal_result'] = sum(decimal_operands)
            elif operation == 'multiply':
                decimal_result = Decimal('1')
                for op in decimal_operands:
                    decimal_result *= op
                result['decimal_result'] = decimal_result
            
            # 计算精度损失
            float_val = result['float_result']
            decimal_val = float(result['decimal_result'])
            
            result['precision_loss'] = abs(float_val - decimal_val)
            if decimal_val != 0:
                result['relative_error'] = abs(float_val - decimal_val) / abs(decimal_val)
            
        except Exception as e:
            result['error'] = str(e)
        
        return result
    
    def benchmark_operations(self, iterations: int = 100000) -> dict:
        """基准测试各种浮点数操作"""
        import time
        
        test_data = [0.1, 0.2, 0.3, 0.4, 0.5] * (iterations // 5)
        results = {}
        
        # 测试普通float求和
        start_time = time.perf_counter()
        float_sum = sum(test_data)
        results['float_sum_time'] = time.perf_counter() - start_time
        results['float_sum_result'] = float_sum
        
        # 测试Kahan求和
        start_time = time.perf_counter()
        kahan_sum = self.safe_sum(test_data)
        results['kahan_sum_time'] = time.perf_counter() - start_time
        results['kahan_sum_result'] = kahan_sum
        
        # 测试Decimal求和
        start_time = time.perf_counter()
        decimal_data = [Decimal(str(x)) for x in test_data]
        decimal_sum = sum(decimal_data)
        results['decimal_sum_time'] = time.perf_counter() - start_time
        results['decimal_sum_result'] = float(decimal_sum)
        
        return results

# 综合示例：Python开发中的最佳实践
def comprehensive_example():
    """综合示例：展示所有技术的实际应用"""
    manager = FloatPrecisionManager()
    
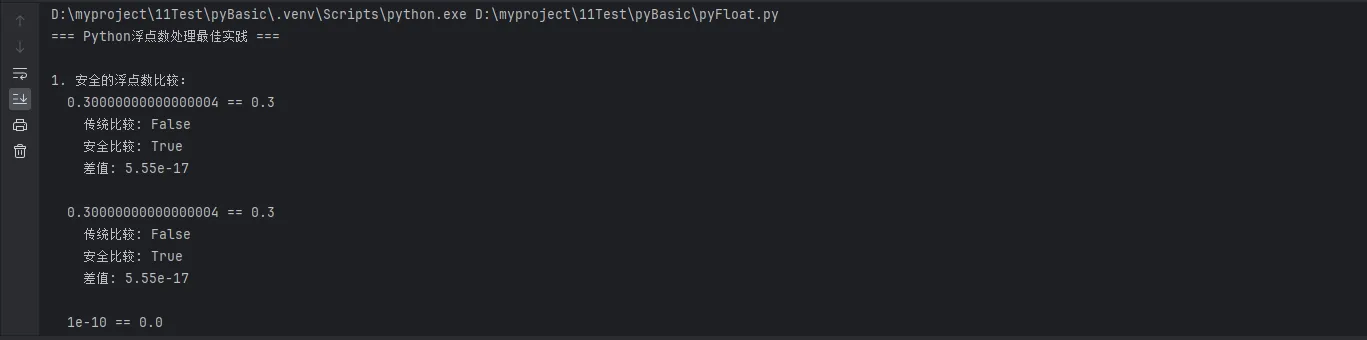
    print("=== Python浮点数处理最佳实践 ===\n")
    
    # 1. 基本比较操作
    print("1. 安全的浮点数比较：")
    test_pairs = [
        (0.1 + 0.2, 0.3),
        (0.1 * 3, 0.3),
        (1e-10, 0.0),
        (math.pi, 22/7)
    ]
    
    for a, b in test_pairs:
        unsafe_equal = (a == b)
        safe_equal = manager.safe_compare(a, b)
        print(f"  {a} == {b}")
        print(f"    传统比较: {unsafe_equal}")
        print(f"    安全比较: {safe_equal}")
        print(f"    差值: {abs(a-b):.2e}")
        print()
    
    # 2. 精度损失分析
    print("2. 精度损失分析：")
    test_operations = [
        ('add', [0.1, 0.2, 0.3]),
        ('multiply', [0.1, 0.1, 0.1]),
        ('add', [1e-16] * 1000)  # 累积误差测试
    ]
    
    for op, operands in test_operations:
        analysis = manager.analyze_precision_loss(op, operands)
        print(f"  操作: {op}({operands[:3]}{'...' if len(operands) > 3 else ''})")
        print(f"    Float结果: {analysis['float_result']}")
        print(f"    Decimal结果: {analysis['decimal_result']}")
        print(f"    精度损失: {analysis['precision_loss']:.2e}")
        if analysis['relative_error']:
            print(f"    相对误差: {analysis['relative_error']:.2e}")
        print()
    
    # 3. 性能基准测试
    print("3. 性能基准测试：")
    benchmark = manager.benchmark_operations(50000)
    
    print(f"  数据规模: 50000个浮点数")
    print(f"  Float求和: {benchmark['float_sum_result']:.10f} "
          f"(耗时: {benchmark['float_sum_time']:.6f}s)")
    print(f"  Kahan求和: {benchmark['kahan_sum_result']:.10f} "
          f"(耗时: {benchmark['kahan_sum_time']:.6f}s)")
    print(f"  Decimal求和: {benchmark['decimal_sum_result']:.10f} "
          f"(耗时: {benchmark['decimal_sum_time']:.6f}s)")
    
    # 4. 实际应用建议
    print("\n4. 实际应用建议：")
    recommendations = [
        "💡 日常计算：使用 math.isclose() 进行浮点数比较",
        "💰 金融计算：使用 decimal 模块确保精度",
        "🔬 科学计算：根据精度要求选择合适的数据类型",
        "⚡ 性能优先：大量计算时考虑使用 numpy 的优化算法",
        "🐛 调试技巧：使用 sys.float_info 了解浮点数限制"
    ]
    
    for rec in recommendations:
        print(f"  {rec}")

comprehensive_example()

🎯 总结与最佳实践

通过本文的深入探讨，我们全面了解了Python浮点数的核心知识点。让我们总结三个关键要点：

核心要点回顾：

1. 🔬 IEEE 754标准理解：浮点数精度问题源于二进制表示的局限性，不是Python的缺陷，而是计算机科学的基本特征。掌握这一点是正确使用浮点数的基础。
2. 🛠️ 精度处理方案：针对不同场景选择合适的解决方案 - math.isclose()适用于一般比较，decimal模块适合金融计算，自定义工具类满足特殊需求。
3. 💡 实战应用技巧：在Windows上位机开发和数据处理中，建立完善的浮点数处理机制不仅能避免计算错误，还能提升代码的健壮性和可维护性。

掌握这些Python开发技巧，将让你在编程实践中更加得心应手，特别是在处理精确计算和数值分析任务时。继续关注我们的技术分享，获取更多实用的Python编程技巧和上位机开发最佳实践！

📚 延伸学习建议：深入学习NumPy数组计算、SciPy科学计算库，以及在工业控制系统中的数值稳定性设计模式。