在Python开发的世界里，整数(int)看似简单，但却蕴含着强大的功能。无论你是刚入门的新手，还是经验丰富的开发者，都可能在整数处理上遇到困惑：为什么Python的整数可以无限大？二进制、八进制、十六进制到底怎么用？在Windows下做上位机开发时，如何高效处理各种进制的数据？

本文将带你深入了解Python整数的核心特性，掌握任意精度计算、进制转换等实战技巧，让你在面对复杂的数值计算和数据处理时游刃有余。

🔍 Python整数的独特之处

任意精度：告别整数溢出的烦恼

与C++、Java等语言不同，Python的整数类型支持任意精度，这意味着你永远不用担心整数溢出问题。

Python
# 在其他语言中可能溢出的超大数
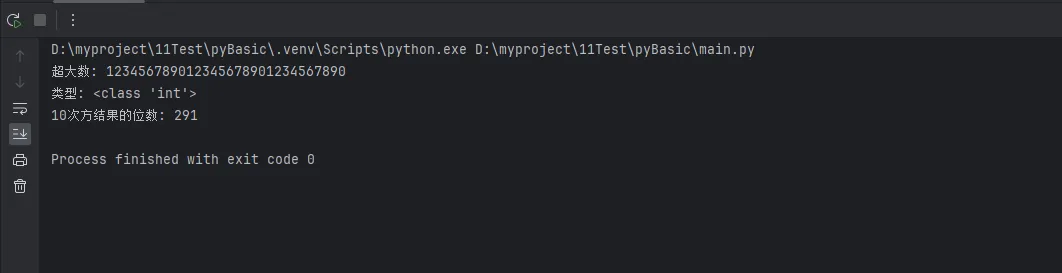
big_number = 123456789012345678901234567890
print(f"超大数: {big_number}")
print(f"类型: {type(big_number)}")

# 进行大数运算
result = big_number ** 10
print(f"10次方结果的位数: {len(str(result))}")

实战应用场景：

• 金融计算：处理大额资金时避免精度丢失
• 密码学：RSA加密中的大素数运算
• 上位机开发：处理传感器的超高精度数据

🎯 内存优化：小整数池机制

Python为了提高性能，对小整数（-5到256）使用了对象池技术：

Python
# 小整数对象复用演示
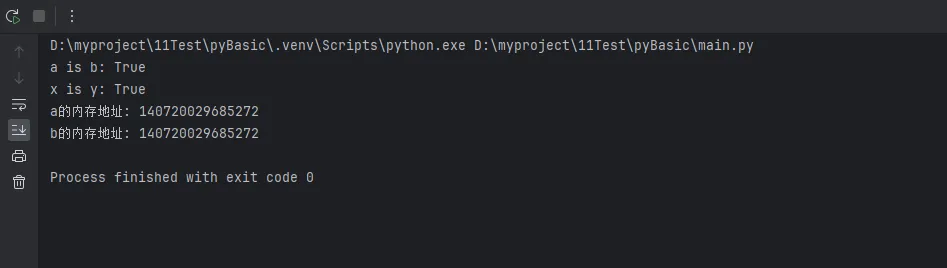
a = 100
b = 100
print(f"a is b: {a is b}")  # True，指向同一对象

# 大整数每次创建新对象
x = 1000
y = 1000
print(f"x is y: {x is y}")  # False，不同对象

# 验证对象ID
print(f"a的内存地址: {id(a)}")
print(f"b的内存地址: {id(b)}")

🚀 进制表示法深度解析

二进制(Binary)：0b前缀

在上位机开发中，二进制操作极其常见，特别是处理设备状态位时：

Python
# 二进制字面量
status_register = 0b11010110  # 214 in decimal

# 实战：解析设备状态位
def parse_device_status(status):
    """解析8位设备状态寄存器"""
    return {
        'power_on': bool(status & 0b00000001),      # 位0：电源状态
        'connected': bool(status & 0b00000010),     # 位1：连接状态
        'error': bool(status & 0b00000100),         # 位2：错误标志
        'ready': bool(status & 0b00001000),         # 位3：就绪状态
        'data_valid': bool(status & 0b00010000),    # 位4：数据有效
    }

# 使用示例
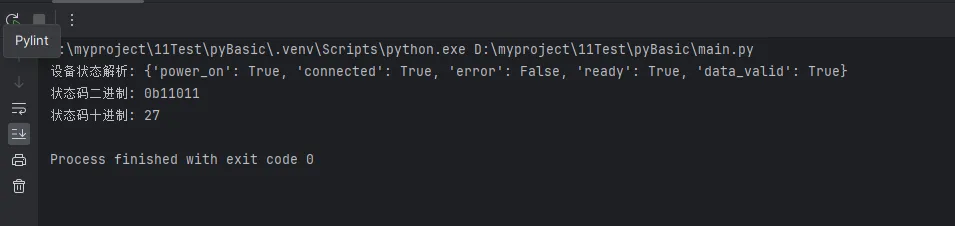
device_status = 0b00011011  # 设备状态
status_info = parse_device_status(device_status)
print("设备状态解析:", status_info)

# 输出二进制表示
print(f"状态码二进制: {bin(device_status)}")
print(f"状态码十进制: {device_status}")

八进制(Octal)：0o前缀

八进制在文件权限设置中广泛应用：

Python
# 文件权限的八进制表示
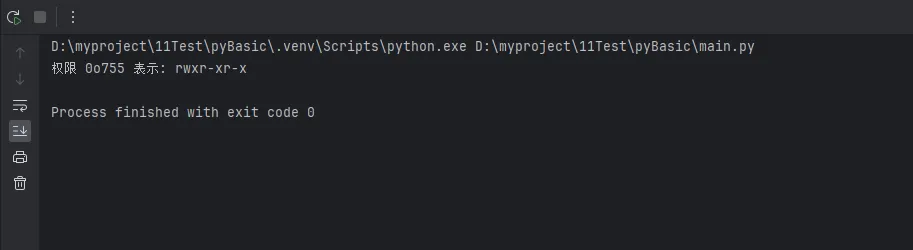
file_permission = 0o755  # rwxr-xr-x

def explain_permission(perm):
    """解释文件权限"""
    owner = (perm >> 6) & 0o7
    group = (perm >> 3) & 0o7
    other = perm & 0o7
    
    def perm_to_string(p):
        return ''.join([
            'r' if p & 4 else '-',
            'w' if p & 2 else '-',
            'x' if p & 1 else '-'
        ])
    
    return f"{perm_to_string(owner)}{perm_to_string(group)}{perm_to_string(other)}"

print(f"权限 {oct(file_permission)} 表示: {explain_permission(file_permission)}")

十六进制(Hexadecimal)：0x前缀

十六进制在颜色处理、内存地址、协议解析中不可或缺：

Python
# 颜色值处理
color_red = 0xFF0000
color_green = 0x00FF00
color_blue = 0x0000FF

def rgb_to_components(color):
    """提取RGB颜色分量"""
    red = (color >> 16) & 0xFF
    green = (color >> 8) & 0xFF
    blue = color & 0xFF
    return red, green, blue

# 混合颜色
purple = 0xFF00FF
r, g, b = rgb_to_components(purple)
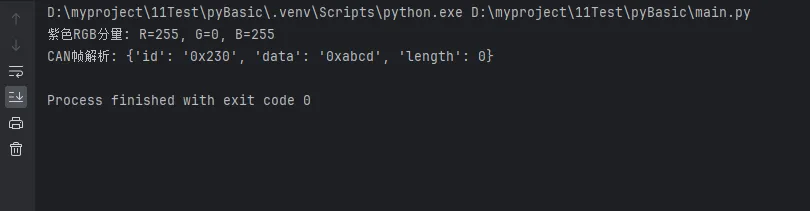
print(f"紫色RGB分量: R={r}, G={g}, B={b}")

# 协议数据解析示例
def parse_can_frame(data):
    """解析CAN总线数据帧"""
    frame_id = (data >> 32) & 0x7FF
    data_bytes = data & 0xFFFFFFFF
    return {
        'id': hex(frame_id),
        'data': hex(data_bytes),
        'length': (data >> 28) & 0xF
    }

can_data = 0x12300000ABCD
frame_info = parse_can_frame(can_data)
print("CAN帧解析:", frame_info)

💡 进制转换实战技巧

🔥 万能转换函数

Python
def number_converter(value, from_base=10, to_base=10):
    """
    通用进制转换器
    支持2-36进制之间的任意转换
    """
    if isinstance(value, str):
        # 字符串转十进制
        decimal = int(value, from_base)
    else:
        decimal = value
    
    if to_base == 10:
        return decimal
    elif to_base == 2:
        return bin(decimal)
    elif to_base == 8:
        return oct(decimal)
    elif to_base == 16:
        return hex(decimal)
    else:
        # 自定义进制转换
        if decimal == 0:
            return "0"
        
        digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
        result = ""
        
        while decimal > 0:
            result = digits[decimal % to_base] + result
            decimal //= to_base
        
        return result

# 使用示例
print("二进制1010转十进制:", number_converter("1010", 2, 10))
print("十进制255转十六进制:", number_converter(255, 10, 16))
print("十六进制FF转二进制:", number_converter("FF", 16, 2))

⚡ 批量进制显示

Python
def show_all_formats(number):
    """显示数字的所有常用进制格式"""
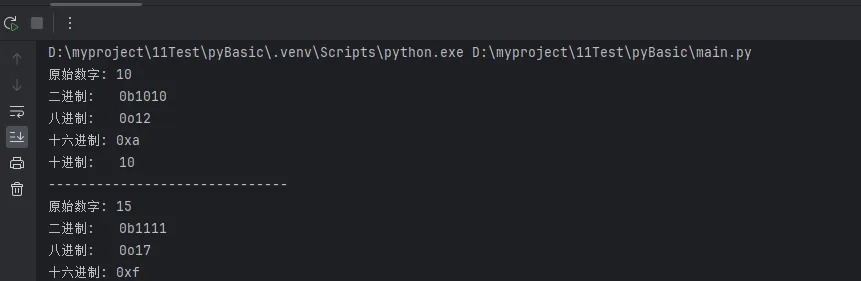
    print(f"原始数字: {number}")
    print(f"二进制:   {bin(number)}")
    print(f"八进制:   {oct(number)}")
    print(f"十六进制: {hex(number)}")
    print(f"十进制:   {number}")
    print("-" * 30)

# 批量展示
test_numbers = [0b1010, 0o17, 0xFF, 255]
for num in test_numbers:
    show_all_formats(num)

🛠️ 实际项目应用案例

案例1：串口通信数据解析

Python
class SerialDataParser:
    """串口数据解析器"""

    def __init__(self):
        self.frame_header = 0xAA55  # 帧头

    def parse_frame(self, raw_data):
        """解析数据帧"""
        # 检查帧头
        if (raw_data >> 16) & 0xFFFF != self.frame_header:
            return None

        # 提取数据字段
        command = (raw_data >> 12) & 0xF
        data_length = (raw_data >> 8) & 0xF
        payload = raw_data & 0xFF

        return {
            'header': hex(self.frame_header),
            'command': command,
            'length': data_length,
            'data': payload
        }

    def create_frame(self, command, data):
        """创建数据帧"""
        # Assuming data is an integer, set length to 1
        data_length = 1
        frame = (self.frame_header << 16) | (command << 12) | (data_length << 8) | data
        return frame


# 使用示例
parser = SerialDataParser()
frame = parser.create_frame(0x5, 0x88)
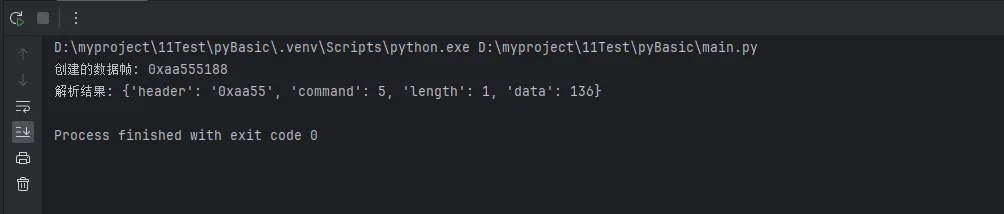
print(f"创建的数据帧: {hex(frame)}")
parsed = parser.parse_frame(frame)
print("解析结果:", parsed)

案例2：位操作工具类

Python
class BitOperations:
    """位操作工具类"""
    
    @staticmethod
    def set_bit(number, position):
        """设置指定位为1"""
        return number | (1 << position)
    
    @staticmethod
    def clear_bit(number, position):
        """清除指定位为0"""
        return number & ~(1 << position)
    
    @staticmethod
    def toggle_bit(number, position):
        """翻转指定位"""
        return number ^ (1 << position)
    
    @staticmethod
    def check_bit(number, position):
        """检查指定位是否为1"""
        return bool(number & (1 << position))
    
    @staticmethod
    def show_bits(number, width=8):
        """显示二进制位表示"""
        return f"{number:0{width}b}"

# 实战演示
bits = BitOperations()
value = 0b10101010

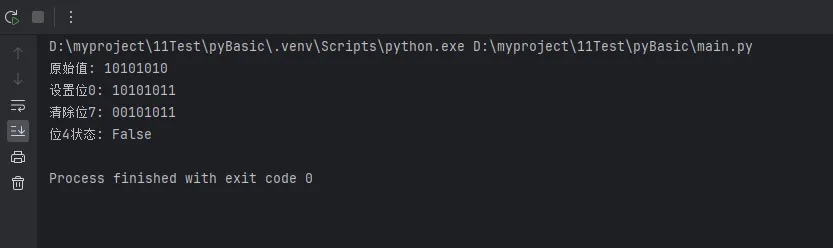
print(f"原始值: {bits.show_bits(value)}")
value = bits.set_bit(value, 0)
print(f"设置位0: {bits.show_bits(value)}")
value = bits.clear_bit(value, 7)
print(f"清除位7: {bits.show_bits(value)}")
print(f"位4状态: {bits.check_bit(value, 4)}")

⚠️ 常见陷阱与最佳实践

陷阱1：进制字面量的易错写法

Python
# ❌ 错误写法
# octal_wrong = 0123  # Python 3中会报错

# ✅ 正确写法
octal_correct = 0o123
binary_correct = 0b1010
hex_correct = 0xFF

print(f"八进制0o123 = {octal_correct}")
print(f"二进制0b1010 = {binary_correct}")  
print(f"十六进制0xFF = {hex_correct}")

陷阱2：整数除法的精度问题

Python
# 整数除法在Python 3中的行为
result1 = 7 / 3    # 真除法，返回float
result2 = 7 // 3   # 整数除法，返回int

print(f"7 / 3 = {result1} (类型: {type(result1)})")
print(f"7 // 3 = {result2} (类型: {type(result2)})")

# 大数除法保持精度
big_num = 10**100
division_result = big_num // 7
print(f"大数整除结果位数: {len(str(division_result))}")

🎯 性能优化建议

Python
# 使用位运算替代数学运算（在适当场景下）
def fast_multiply_by_power_of_2(number, power):
    """使用位移快速乘以2的幂"""
    return number << power


def fast_divide_by_power_of_2(number, power):
    """使用位移快速除以2的幂"""
    return number >> power


# 性能对比
import time


def performance_test():
    """性能测试"""
    test_num = 123456789
    iterations = 1000000

    # 传统乘法
    start_time = time.time()
    for _ in range(iterations):
        result = test_num * 8
    traditional_time = time.time() - start_time

    # 位运算
    start_time = time.time()
    for _ in range(iterations):
        result = fast_multiply_by_power_of_2(test_num, 3)  # 乘以2^3=8
    bit_operation_time = time.time() - start_time

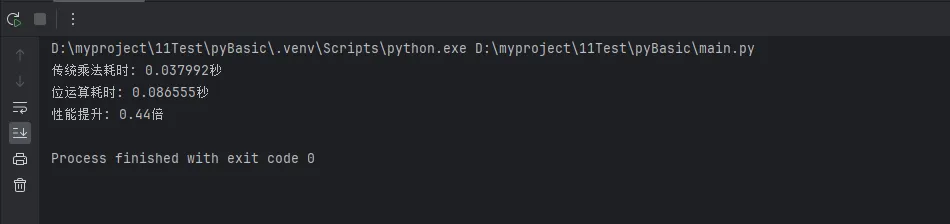
    print(f"传统乘法耗时: {traditional_time:.6f}秒")
    print(f"位运算耗时: {bit_operation_time:.6f}秒")
    print(f"性能提升: {traditional_time / bit_operation_time:.2f}倍")

performance_test()

🎯 核心要点总结

通过本文的深入讲解，我们全面掌握了Python整数类型的三个核心特性：

1. 任意精度支持：Python整数永远不会溢出，为大数运算和高精度计算提供了强大保障，特别适合金融、科学计算等对精度要求极高的场景。
2. 多进制表示法：熟练运用二进制(0b)、八进制(0o)、十六进制(0x)表示法，能让我们在上位机开发、协议解析、硬件接口等专业领域游刃有余。
3. 高效位操作：掌握位运算技巧不仅能提升代码性能，更是处理底层数据、状态控制的必备技能。

在实际的Python开发工作中，深入理解整数类型的这些特性，将帮助你写出更高效、更专业的代码。特别是在Windows环境下进行上位机开发时，这些知识将成为你解决复杂数据处理问题的有力武器。

记住：编程不仅仅是语法的堆砌，更是对数据本质的深刻理解。从今天开始，让我们用更专业的视角来运用Python的每一个数据类型！