作为Python开发者，数据可视化是我们日常工作中不可或缺的技能。无论是分析业务数据、展示项目成果，还是进行科学计算，Matplotlib都是我们的得力助手。但你是否曾经为plot()函数的各种参数而困惑？为什么同样的数据，别人画出的图表就是比你的更专业、更美观？

今天这篇文章将彻底解决这些问题。我们将从plot()函数的核心参数开始，深入讲解线条样式、颜色设置、标记符号的使用技巧，掌握多条曲线的绘制方法，最后通过实战案例绘制数学函数图像。让你的数据可视化技能从此脱胎换骨！

🔍 plot()函数核心参数解析

基础语法结构

Python
import matplotlib.pyplot as plt
import numpy as np

# 基础语法
plt.plot(x, y, format_string, **kwargs)

plot()函数的核心在于理解其参数结构：

• x, y：数据点的坐标
• format_string：格式化字符串，控制线条样式
• kwargs：关键字参数，提供更精细的控制

🎨 线条样式与颜色大全

线条样式参数详解

Python
import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体支持
# Windows下的字体和显示优化
plt.rcParams['font.sans-serif'] = ['SimHei','Microsoft YaHei']  # 支持中文显示
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题
plt.rcParams['figure.autolayout'] = True     # 自动调整布局
plt.rcParams['savefig.dpi'] = 300            # 默认保存分辨率

# 使用标准后端而不是PyCharm的后端
import matplotlib
matplotlib.use('TkAgg')

# 生成示例数据
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x + np.pi/4)

# 创建子图展示不同线条样式
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
fig.suptitle('线条样式大全', fontsize=16, fontweight='bold')

# 实线样式
axes[0,0].plot(x, y1, '-', label='实线 (-)')
axes[0,0].plot(x, y2, '--', label='虚线 (--)')
axes[0,0].plot(x, y3, '-.', label='点划线 (-.)')
axes[0,0].set_title('🔥 基础线条样式')
axes[0,0].legend()
axes[0,0].grid(True, alpha=0.3)

# 线宽控制
axes[0,1].plot(x, y1, linewidth=1, label='线宽=1')
axes[0,1].plot(x, y2, linewidth=3, label='线宽=3')
axes[0,1].plot(x, y3, linewidth=5, label='线宽=5')
axes[0,1].set_title('📏 线宽控制')
axes[0,1].legend()
axes[0,1].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

颜色设置的多种方式

Python
import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体支持
# Windows下的字体和显示优化
plt.rcParams['font.sans-serif'] = ['SimHei','Microsoft YaHei']  # 支持中文显示
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题
plt.rcParams['figure.autolayout'] = True     # 自动调整布局
plt.rcParams['savefig.dpi'] = 300            # 默认保存分辨率

# 使用标准后端而不是PyCharm的后端
import matplotlib
matplotlib.use('TkAgg')

# 生成示例数据
x = np.linspace(0, 10, 100)
y1 = np.sin(x)
y2 = np.cos(x)
y3 = np.sin(x + np.pi/4)


# 颜色设置的6种方法
fig, ax = plt.subplots(figsize=(10, 6))

# 方法1：单字母简写
ax.plot(x, y1, 'r-', label='红色 (r)')

# 方法2：英文名称
ax.plot(x, y1+0.5, color='blue', label='蓝色 (blue)')

# 方法3：十六进制
ax.plot(x, y1+1.0, color='#FF5733', label='橙色 (#FF5733)')

# 方法4：RGB元组
ax.plot(x, y1+1.5, color=(0.2, 0.8, 0.2), label='绿色 (RGB)')

# 方法5：灰度值
ax.plot(x, y1+2.0, color='0.7', label='灰色 (0.7)')

# 方法6：预定义颜色映射
colors = plt.cm.viridis(np.linspace(0, 1, 3))
for i, color in enumerate(colors):
    ax.plot(x, y1+2.5+i*0.3, color=color, label=f'viridis_{i}')

ax.set_title('🌈 颜色设置方法大全')
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()

🎯 标记符号的艺术

标记符号能让数据点更加突出，特别适合数据量较少的情况。

Python
import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体支持
# Windows下的字体和显示优化
plt.rcParams['font.sans-serif'] = ['SimHei','Microsoft YaHei']  # 支持中文显示
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题
plt.rcParams['figure.autolayout'] = True     # 自动调整布局
plt.rcParams['savefig.dpi'] = 300            # 默认保存分辨率

# 使用标准后端而不是PyCharm的后端
import matplotlib
matplotlib.use('TkAgg')

# 标记符号展示
fig, axes = plt.subplots(1, 2, figsize=(14, 5))

# 常用标记符号
x_short = np.linspace(0, 10, 20)
y_short = np.sin(x_short)

markers = ['o', 's', '^', 'v', 'D', '*', '+', 'x']
marker_names = ['圆形', '方形', '上三角', '下三角', '菱形', '星形', '加号', '叉号']

for i, (marker, name) in enumerate(zip(markers, marker_names)):
    axes[0].plot(x_short, y_short + i*0.3,
                marker=marker,
                markersize=8,
                label=f'{name} ({marker})',
                linewidth=1)

axes[0].set_title('🔍 标记符号类型')
axes[0].legend()
axes[0].grid(True, alpha=0.3)

# 标记样式自定义
axes[1].plot(x_short, y_short, 'o-',
            markersize=10,
            markerfacecolor='red',
            markeredgecolor='blue',
            markeredgewidth=2,
            linewidth=2,
            label='自定义标记')

axes[1].plot(x_short, y_short+0.5, 's--',
            markersize=8,
            markerfacecolor='none',
            markeredgecolor='green',
            markeredgewidth=2,
            label='空心标记')

axes[1].set_title('🎨 标记样式自定义')
axes[1].legend()
axes[1].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

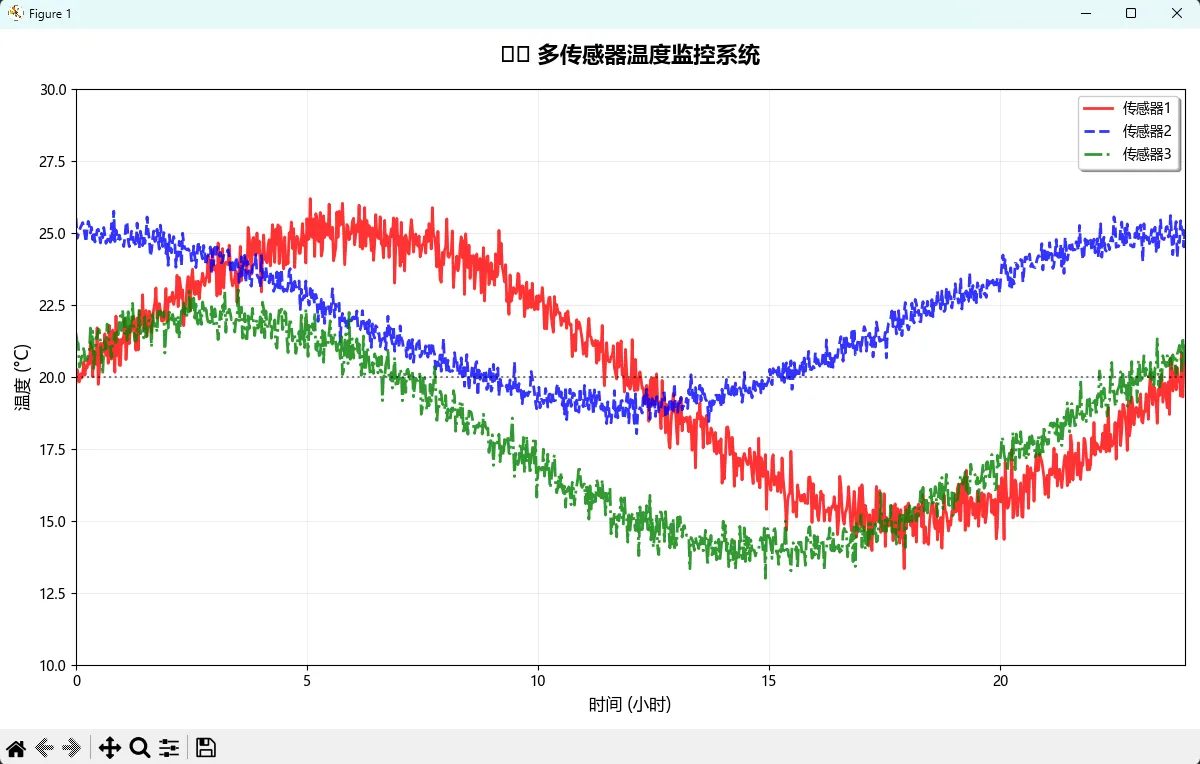
📊 多条曲线绘制技巧

在实际的Python开发项目中，我们经常需要在同一图表中展示多条曲线进行对比分析。

Python
import matplotlib.pyplot as plt
import numpy as np

# 设置中文字体支持
# Windows下的字体和显示优化
plt.rcParams['font.sans-serif'] = ['SimHei','Microsoft YaHei']  # 支持中文显示
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题
plt.rcParams['figure.autolayout'] = True     # 自动调整布局
plt.rcParams['savefig.dpi'] = 300            # 默认保存分辨率

# 使用标准后端而不是PyCharm的后端
import matplotlib
matplotlib.use('TkAgg')  # 或者 'Qt5Agg'


# 多条曲线绘制的最佳实践
def plot_multiple_curves():
    """
    多条曲线绘制函数
    适用于上位机开发中的多传感器数据对比
    """
    # 模拟传感器数据
    time = np.linspace(0, 24, 1000)  # 24小时
    temp_sensor1 = 20 + 5 * np.sin(2 * np.pi * time / 24) + np.random.normal(0, 0.5, 1000)
    temp_sensor2 = 22 + 3 * np.cos(2 * np.pi * time / 24) + np.random.normal(0, 0.3, 1000)
    temp_sensor3 = 18 + 4 * np.sin(2 * np.pi * time / 24 + np.pi / 4) + np.random.normal(0, 0.4, 1000)

    # 创建图表
    plt.figure(figsize=(12, 7))

    # 方法1：分别调用plot()
    plt.plot(time, temp_sensor1, 'r-', linewidth=2, label='传感器1', alpha=0.8)
    plt.plot(time, temp_sensor2, 'b--', linewidth=2, label='传感器2', alpha=0.8)
    plt.plot(time, temp_sensor3, 'g-.', linewidth=2, label='传感器3', alpha=0.8)

    # 图表美化
    plt.title('🌡️ 多传感器温度监控系统', fontsize=16, fontweight='bold', pad=20)
    plt.xlabel('时间 (小时)', fontsize=12)
    plt.ylabel('温度 (°C)', fontsize=12)
    plt.legend(loc='upper right', frameon=True, fancybox=True, shadow=True)
    plt.grid(True, alpha=0.3, linestyle='-', linewidth=0.5)

    # 设置坐标轴范围
    plt.xlim(0, 24)
    plt.ylim(10, 30)

    # 添加水平参考线
    plt.axhline(y=20, color='k', linestyle=':', alpha=0.5, label='目标温度')

    plt.tight_layout()
    plt.show()


# 执行函数
plot_multiple_curves()

高级多曲线技巧

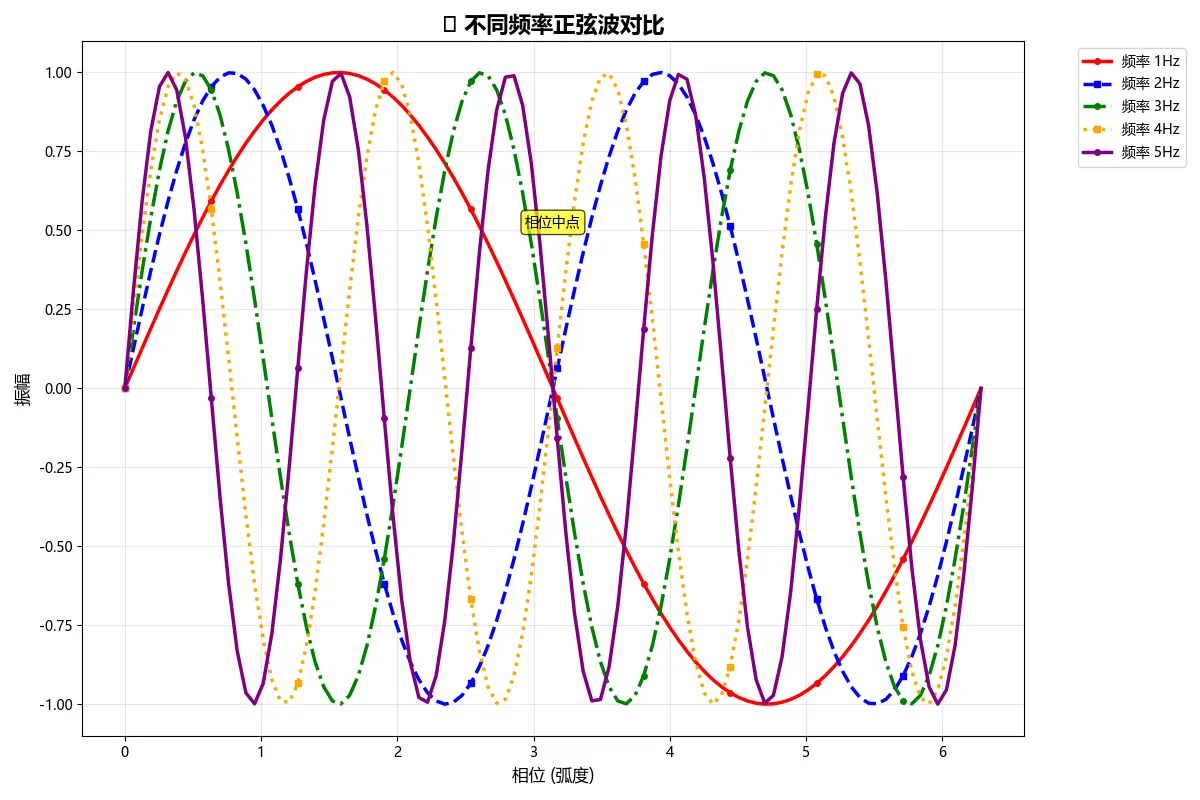
Python
# 使用循环批量绘制
def advanced_multiple_plots():
    """
    高级多曲线绘制技巧
    适合处理大量数据系列
    """
    # 生成多组数据
    x = np.linspace(0, 2*np.pi, 100)
    frequencies = [1, 2, 3, 4, 5]
    colors = ['red', 'blue', 'green', 'orange', 'purple']
    line_styles = ['-', '--', '-.', ':', '-']
    
    plt.figure(figsize=(12, 8))
    
    # 使用zip和enumerate进行批量绘制
    for i, (freq, color, style) in enumerate(zip(frequencies, colors, line_styles)):
        y = np.sin(freq * x)
        plt.plot(x, y, 
                color=color, 
                linestyle=style, 
                linewidth=2.5,
                marker='o' if i % 2 == 0 else 's',  # 交替使用标记
                markersize=4,
                markevery=10,  # 每10个点标记一次
                label=f'频率 {freq}Hz')
    
    # 专业图表设置
    plt.title('🎵 不同频率正弦波对比', fontsize=16, fontweight='bold')
    plt.xlabel('相位 (弧度)', fontsize=12)
    plt.ylabel('振幅', fontsize=12)
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
    plt.grid(True, alpha=0.3)
    
    # 添加文本注释
    plt.text(np.pi, 0.5, '相位中点', 
            fontsize=10, ha='center', va='bottom',
            bbox=dict(boxstyle='round,pad=0.3', facecolor='yellow', alpha=0.7))
    
    plt.tight_layout()
    plt.show()

advanced_multiple_plots()

🚀 实战案例：数学函数图像绘制

让我们通过一个完整的实战案例，展示如何绘制复杂的数学函数图像。这在科学计算和工程应用中非常实用。

Python
import matplotlib

# 必须在导入pyplot之前设置后端
matplotlib.use('TkAgg')

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.font_manager as fm


def setup_chinese_fonts():
    """设置中文字体支持"""
    # 查找系统可用字体
    available_fonts = [f.name for f in fm.fontManager.ttflist]

    # Windows常用中文字体列表（按优先级）
    chinese_fonts = [
        'Microsoft YaHei',  # 微软雅黑
        'SimHei',  # 黑体
        'SimSun',  # 宋体
        'KaiTi',  # 楷体
        'FangSong',  # 仿宋
        'Microsoft JhengHei'  # 微软正黑体
    ]

    # 找到第一个可用的中文字体
    selected_font = None
    for font in chinese_fonts:
        if font in available_fonts:
            selected_font = font
            break

    if selected_font:
        print(f"✅ 找到中文字体: {selected_font}")
        # 设置字体
        plt.rcParams['font.sans-serif'] = [selected_font]
        plt.rcParams['axes.unicode_minus'] = False
        plt.rcParams['figure.autolayout'] = True
        plt.rcParams['savefig.dpi'] = 300
        return True
    else:
        print("❌ 未找到中文字体，使用英文标题")
        plt.rcParams['font.sans-serif'] = ['DejaVu Sans']
        return False


class MathFunctionPlotter:
    """
    数学函数绘图器
    适用于教学、科研和工程计算可视化
    """

    def __init__(self, figsize=(15, 10)):
        self.figsize = figsize
        self.has_chinese = setup_chinese_fonts()

    def get_title(self, chinese_title, english_title):
        """根据字体支持情况返回合适的标题"""
        return chinese_title if self.has_chinese else english_title

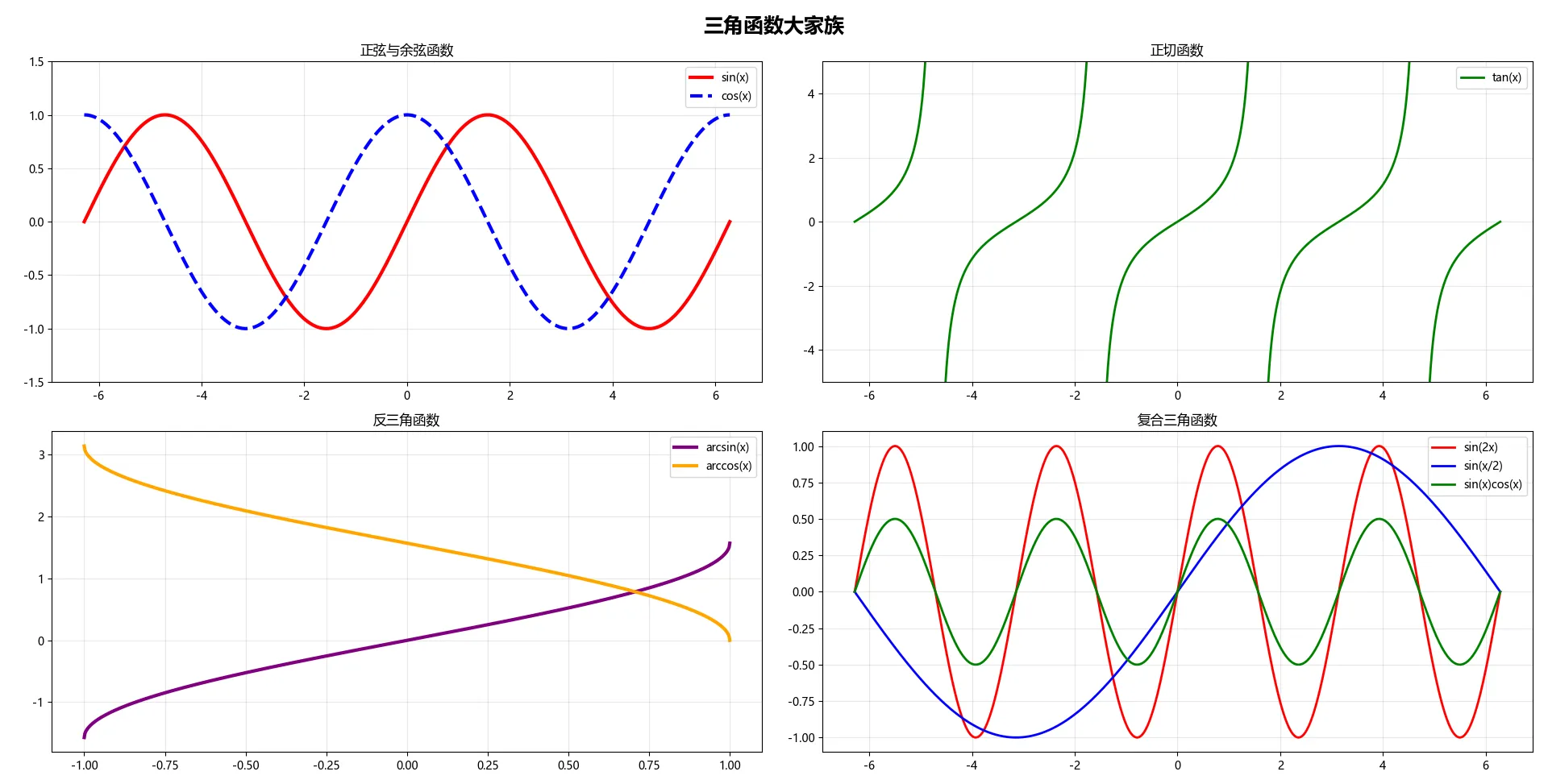
    def plot_trigonometric_functions(self):
        """绘制三角函数族"""
        x = np.linspace(-2 * np.pi, 2 * np.pi, 1000)

        fig, axes = plt.subplots(2, 2, figsize=self.figsize)
        fig.suptitle(self.get_title('三角函数大家族', 'Trigonometric Functions'),
                     fontsize=18, fontweight='bold', y=0.98)

        # sin和cos
        axes[0, 0].plot(x, np.sin(x), 'r-', linewidth=3, label='sin(x)')
        axes[0, 0].plot(x, np.cos(x), 'b--', linewidth=3, label='cos(x)')
        axes[0, 0].set_title(self.get_title('正弦与余弦函数', 'Sine and Cosine'))
        axes[0, 0].legend()
        axes[0, 0].grid(True, alpha=0.3)
        axes[0, 0].set_ylim(-1.5, 1.5)

        # tan函数（处理渐近线）
        x_tan = np.linspace(-2 * np.pi, 2 * np.pi, 10000)
        y_tan = np.tan(x_tan)
        # 限制y值范围避免渐近线影响
        y_tan[np.abs(y_tan) > 10] = np.nan
        axes[0, 1].plot(x_tan, y_tan, 'g-', linewidth=2, label='tan(x)')
        axes[0, 1].set_title(self.get_title('正切函数', 'Tangent Function'))
        axes[0, 1].set_ylim(-5, 5)
        axes[0, 1].legend()
        axes[0, 1].grid(True, alpha=0.3)

        # 反三角函数
        x_arc = np.linspace(-1, 1, 1000)
        axes[1, 0].plot(x_arc, np.arcsin(x_arc), 'purple', linewidth=3, label='arcsin(x)')
        axes[1, 0].plot(x_arc, np.arccos(x_arc), 'orange', linewidth=3, label='arccos(x)')
        axes[1, 0].set_title(self.get_title('反三角函数', 'Inverse Trigonometric'))
        axes[1, 0].legend()
        axes[1, 0].grid(True, alpha=0.3)

        # 复合三角函数
        axes[1, 1].plot(x, np.sin(2 * x), 'red', linewidth=2, label='sin(2x)')
        axes[1, 1].plot(x, np.sin(x / 2), 'blue', linewidth=2, label='sin(x/2)')
        axes[1, 1].plot(x, np.sin(x) * np.cos(x), 'green', linewidth=2, label='sin(x)cos(x)')
        axes[1, 1].set_title(self.get_title('复合三角函数', 'Composite Functions'))
        axes[1, 1].legend()
        axes[1, 1].grid(True, alpha=0.3)

        plt.tight_layout()
        plt.show()

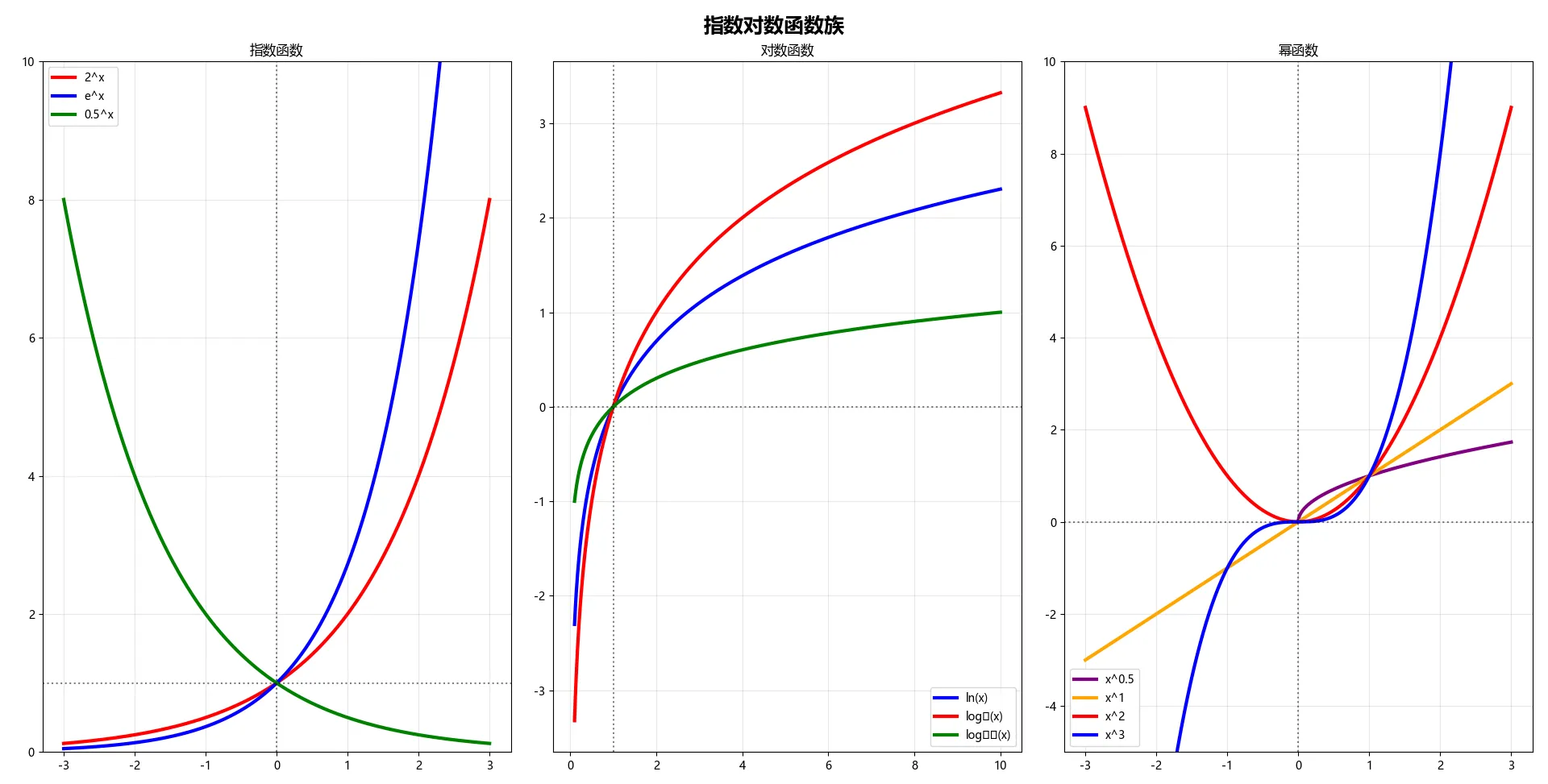
    def plot_exponential_logarithmic(self):
        """绘制指数对数函数"""
        fig, axes = plt.subplots(1, 3, figsize=self.figsize)
        fig.suptitle(self.get_title('指数对数函数族', 'Exponential & Logarithmic Functions'),
                     fontsize=18, fontweight='bold')

        # 指数函数
        x1 = np.linspace(-3, 3, 1000)
        bases = [2, np.e, 0.5]
        colors = ['red', 'blue', 'green']
        labels = ['2^x', 'e^x', '0.5^x']

        for base, color, label in zip(bases, colors, labels):
            if base == np.e:
                y = np.exp(x1)
            else:
                y = base ** x1
            axes[0].plot(x1, y, color=color, linewidth=3, label=label)

        axes[0].set_title(self.get_title('指数函数', 'Exponential Functions'))
        axes[0].set_ylim(0, 10)
        axes[0].legend()
        axes[0].grid(True, alpha=0.3)
        axes[0].axhline(y=1, color='k', linestyle=':', alpha=0.5)
        axes[0].axvline(x=0, color='k', linestyle=':', alpha=0.5)

        # 对数函数
        x2 = np.linspace(0.1, 10, 1000)
        axes[1].plot(x2, np.log(x2), 'blue', linewidth=3, label='ln(x)')
        axes[1].plot(x2, np.log2(x2), 'red', linewidth=3, label='log₂(x)')
        axes[1].plot(x2, np.log10(x2), 'green', linewidth=3, label='log₁₀(x)')
        axes[1].set_title(self.get_title('对数函数', 'Logarithmic Functions'))
        axes[1].legend()
        axes[1].grid(True, alpha=0.3)
        axes[1].axhline(y=0, color='k', linestyle=':', alpha=0.5)
        axes[1].axvline(x=1, color='k', linestyle=':', alpha=0.5)

        # 幂函数
        x3 = np.linspace(-3, 3, 1000)
        powers = [0.5, 1, 2, 3]
        colors = ['purple', 'orange', 'red', 'blue']

        for power, color in zip(powers, colors):
            if power == 0.5:
                # 只绘制x>=0的部分
                x_pos = x3[x3 >= 0]
                y = x_pos ** power
                axes[2].plot(x_pos, y, color=color, linewidth=3, label=f'x^{power}')
            else:
                y = x3 ** power
                axes[2].plot(x3, y, color=color, linewidth=3, label=f'x^{power}')

        axes[2].set_title(self.get_title('幂函数', 'Power Functions'))
        axes[2].set_ylim(-5, 10)
        axes[2].legend()
        axes[2].grid(True, alpha=0.3)
        axes[2].axhline(y=0, color='k', linestyle=':', alpha=0.5)
        axes[2].axvline(x=0, color='k', linestyle=':', alpha=0.5)

        plt.tight_layout()
        plt.show()

    def plot_complex_function(self):
        """绘制复杂组合函数"""
        x = np.linspace(-5, 5, 2000)

        plt.figure(figsize=(14, 10))

        # 创建2x2子图
        plt.subplot(2, 2, 1)
        y1 = np.sin(x) * np.exp(-x ** 2 / 10)  # 高斯调制的正弦波
        plt.plot(x, y1, 'red', linewidth=3)
        plt.title(self.get_title('高斯调制正弦波: sin(x)·e^(-x²/10)',
                                 'Gaussian Modulated Sine Wave'),
                  fontsize=12, fontweight='bold')
        plt.grid(True, alpha=0.3)

        plt.subplot(2, 2, 2)
        y2 = x * np.sin(10 * x) / (x ** 2 + 1)  # 振荡衰减函数
        plt.plot(x, y2, 'blue', linewidth=2)
        plt.title(self.get_title('振荡衰减函数: x·sin(10x)/(x²+1)',
                                 'Oscillating Decay Function'),
                  fontsize=12, fontweight='bold')
        plt.grid(True, alpha=0.3)

        plt.subplot(2, 2, 3)
        # 分段函数
        y3 = np.piecewise(x,
                          [x < -1, (x >= -1) & (x < 1), x >= 1],
                          [lambda x: x ** 2, lambda x: -x, lambda x: np.sin(x)])
        plt.plot(x, y3, 'green', linewidth=3)
        plt.title(self.get_title('分段函数', 'Piecewise Function'),
                  fontsize=12, fontweight='bold')
        plt.grid(True, alpha=0.3)

        plt.subplot(2, 2, 4)
        # 参数方程绘制心形
        t = np.linspace(0, 2 * np.pi, 1000)
        x_heart = 16 * np.sin(t) ** 3
        y_heart = 13 * np.cos(t) - 5 * np.cos(2 * t) - 2 * np.cos(3 * t) - np.cos(4 * t)
        plt.plot(x_heart, y_heart, 'red', linewidth=4)
        plt.title(self.get_title('心形曲线 (参数方程)', 'Heart Curve (Parametric)'),
                  fontsize=12, fontweight='bold')
        plt.axis('equal')
        plt.grid(True, alpha=0.3)

        plt.suptitle(self.get_title('复杂数学函数可视化', 'Complex Mathematical Functions'),
                     fontsize=16, fontweight='bold', y=0.98)
        plt.tight_layout()
        plt.show()


def check_font_availability():
    """检查字体可用性"""
    print("🔍 检查系统字体...")
    available_fonts = [f.name for f in fm.fontManager.ttflist]

    chinese_fonts = ['Microsoft YaHei', 'SimHei', 'SimSun', 'KaiTi']

    print("可用的中文字体:")
    found_fonts = []
    for font in chinese_fonts:
        if font in available_fonts:
            found_fonts.append(font)
            print(f"  ✅ {font}")
        else:
            print(f"  ❌ {font}")

    if not found_fonts:
        print("\n⚠️ 未找到中文字体，图表将使用英文标题")
        print("💡 解决方案:")
        print("1. Windows: 确保已安装微软雅黑或黑体")
        print("2. 或运行以下命令安装字体包:")
        print("   pip install matplotlib-cn")

    return len(found_fonts) > 0


# 使用示例
if __name__ == "__main__":
    print("🚀 启动数学函数绘图器...")

    # 检查字体
    has_fonts = check_font_availability()
    print("-" * 50)

    # 创建绘图器
    plotter = MathFunctionPlotter()

    print("📊 开始绘制数学函数图像...")
    try:
        plotter.plot_trigonometric_functions()
        plotter.plot_exponential_logarithmic()
        plotter.plot_complex_function()
        print("✅ 图像绘制完成！")
    except Exception as e:
        print(f"❌ 绘制失败: {e}")
        print("💡 尝试运行字体诊断程序...")

📚 总结与扩展

通过这篇详细的教程，我们深入学习了Python Matplotlib中plot()函数的各种参数和使用技巧。让我们回顾一下三个核心要点：

🎯 参数掌握：从基础的线条样式、颜色设置到高级的标记符号，每个参数都有其特定的使用场景。掌握format_string的简写语法能让你快速创建图表，而kwargs参数则提供了更精细的控制能力。

📊 多曲线技巧：在实际的Python开发项目中，多条曲线对比是常见需求。通过合理使用颜色、线型和标记的组合，可以让数据对比更加清晰直观。记住使用循环和enumerate能大大提高编程效率。

🚀 实战应用：无论是科学计算、数据分析还是上位机开发，数学函数的可视化都是基础技能。通过封装成类的方式，可以提高代码的复用性和维护性。

想要进一步提升你的数据可视化技能吗？建议接下来学习subplot布局管理、3D图形绘制，以及与pandas数据框架的集成使用。这些技能将让你在Python开发道路上更进一步！

记住：好的可视化不仅要准确传达数据信息，更要具备良好的美观性和可读性。多练习、多思考，你一定能创作出令人印象深刻的数据图表！